Układ m równań liniowych z n niewiadomymi zwany systemem formy
Gdzie ij I b ja (I=1,…,M; B=1,…,N) to kilka znanych liczb, i x 1 ,…,x n- nieznany. W wyznaczaniu współczynników ij pierwszy indeks I oznacza numer równania, a drugi J– liczba niewiadomych, przy której stoi ten współczynnik.
Współczynniki niewiadomych zapiszemy w postaci macierzy 
, który nazwiemy macierz układu.
Liczby po prawej stronie równań to b 1 ,…,b m są nazywane wolni członkowie.
Całość N liczby c 1 ,…,c n zwany decyzja danego układu, jeżeli każde równanie układu staje się równością po podstawieniu do niego liczb c 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x n.
Naszym zadaniem będzie znalezienie rozwiązań dla systemu. W takim przypadku mogą zaistnieć trzy sytuacje:
Układ równań liniowych, który ma co najmniej jedno rozwiązanie nazywa się wspólny. W przeciwnym razie, tj. jeśli system nie ma rozwiązań, nazywa się go nie wspólne.
Zastanówmy się, jak znaleźć rozwiązania dla systemu.
METODA MATRYCOWA ROZWIĄZANIA UKŁADÓW RÓWNAŃ LINIOWYCH
Macierze umożliwiają krótkie zapisanie układu równań liniowych. Niech będzie dany układ 3 równań z trzema niewiadomymi:
Rozważmy macierz systemu 
i macierze kolumny nieznanych i wolnych terminów 
Znajdźmy pracę
te. w wyniku iloczynu otrzymujemy lewe strony równań tego układu. Następnie korzystając z definicji równości macierzy układ ten można zapisać w postaci
lub krócej A∙X=B.
Oto macierze A I B są znane, oraz macierz X nieznany. Trzeba go znaleźć, bo... jego elementy są rozwiązaniem tego systemu. To równanie nazywa się równanie macierzowe.
Niech wyznacznik macierzy będzie różny od zera | A| ≠ 0. Następnie równanie macierzowe rozwiązuje się w następujący sposób. Pomnóż obie strony równania po lewej stronie przez macierz A-1, odwrotność macierzy A: . Ponieważ A -1 A = E I mi∙X = X, wówczas otrzymujemy rozwiązanie równania macierzowego w postaci X = A -1 B .
Należy zauważyć, że ponieważ macierz odwrotną można znaleźć tylko dla macierzy kwadratowych, metoda macierzowa może rozwiązać tylko te układy, w których liczba równań pokrywa się z liczbą niewiadomych. Jednakże macierzowy zapis układu jest możliwy również w przypadku, gdy liczba równań nie jest równa liczbie niewiadomych, wówczas macierz A nie będzie kwadratowy i dlatego nie da się znaleźć rozwiązania układu w postaci X = A -1 B.
Przykłady. Rozwiązywać układy równań.
REGUŁA CRAMERA
Rozważmy układ 3 równań liniowych z trzema niewiadomymi:
Wyznacznik trzeciego rzędu odpowiadający macierzy układu, tj. złożony ze współczynników niewiadomych,
zwany wyznacznik systemu.
Skomponujmy jeszcze trzy wyznaczniki w następujący sposób: zamień kolejno 1, 2 i 3 kolumny w wyznaczniku D na kolumnę wolnych terminów
Następnie możemy udowodnić następujący wynik.
Twierdzenie (reguła Cramera). Jeżeli wyznacznik układu Δ ≠ 0, to rozpatrywany układ ma jedno i tylko jedno rozwiązanie, a
Dowód. Rozważmy więc układ trzech równań z trzema niewiadomymi. Pomnóżmy pierwsze równanie układu przez dopełnienie algebraiczne 11 element 11, 2 równanie – włączone 21 i 3. – dalej 31:
Dodajmy te równania:
Przyjrzyjmy się każdemu z nawiasów i prawej stronie tego równania. Według twierdzenia o rozwinięciu wyznacznika w elementach pierwszej kolumny
Podobnie można wykazać, że i .
Wreszcie łatwo to zauważyć 
Otrzymujemy zatem równość: .
Stąd, .
Równości i wyprowadza się w podobny sposób, z czego wynika stwierdzenie twierdzenia.
Zauważamy zatem, że jeśli wyznacznik układu Δ ≠ 0, to układ ma rozwiązanie jednoznaczne i odwrotnie. Jeżeli wyznacznik układu jest równy zero, to układ albo ma nieskończoną liczbę rozwiązań, albo nie ma rozwiązań, tj. niekompatybilny.
Przykłady. Rozwiązać układ równań
METODA GAUssa
Omówione wcześniej metody można zastosować do rozwiązania tylko tych układów, w których liczba równań pokrywa się z liczbą niewiadomych, a wyznacznik układu musi być różny od zera. Metoda Gaussa jest bardziej uniwersalna i odpowiednia dla układów o dowolnej liczbie równań. Polega ona na konsekwentnym eliminowaniu niewiadomych z równań układu.
Rozważmy ponownie układ trzech równań z trzema niewiadomymi:
.
Pierwsze równanie pozostawimy bez zmian, a z drugiego i trzeciego wykluczymy terminy zawierające x 1. Aby to zrobić, podziel drugie równanie przez A 21 i pomnóż przez – A 11, a następnie dodaj go do pierwszego równania. Podobnie dzielimy trzecie równanie przez A 31 i pomnóż przez – A 11, a następnie dodaj go do pierwszego. W efekcie oryginalny system przyjmie postać:
Teraz z ostatniego równania eliminujemy termin zawierający x 2. Aby to zrobić, podziel trzecie równanie przez, pomnóż przez drugie i dodaj z drugim. Wtedy będziemy mieli układ równań:
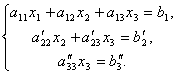
Stąd z ostatniego równania łatwo jest znaleźć x 3, to z drugiego równania x 2 i wreszcie, od 1-go - x 1.
W przypadku stosowania metody Gaussa równania można w razie potrzeby zamienić.
Często zamiast pisać nowy układ równań ograniczają się do napisania rozszerzonej macierzy układu:
a następnie doprowadź go do postaci trójkątnej lub ukośnej za pomocą elementarnych przekształceń.
DO elementarne przemiany macierze obejmują następujące przekształcenia:
- przestawianie wierszy lub kolumn;
- mnożenie ciągu przez liczbę inną niż zero;
- dodanie innych linii do jednej linii.
Przykłady: Rozwiązywać układy równań metodą Gaussa.
Zatem układ ma nieskończoną liczbę rozwiązań.
Układ równań liniowych jest sumą n równań liniowych, z których każde zawiera k zmiennych. Jest napisane tak:
Wielu, spotykając się po raz pierwszy z wyższą algebrą, błędnie uważa, że liczba równań musi koniecznie pokrywać się z liczbą zmiennych. W algebrze szkolnej zwykle tak się dzieje, ale w algebrze wyższej na ogół nie jest to prawdą.
Rozwiązaniem układu równań jest ciąg liczb (k 1, k 2, ..., k n), który jest rozwiązaniem każdego równania układu, czyli: podstawiając do tego równania zamiast zmiennych x 1, x 2, ..., x n otrzymujemy poprawną równość liczbową.
Zatem rozwiązanie układu równań oznacza znalezienie zbioru wszystkich jego rozwiązań lub udowodnienie, że zbiór ten jest pusty. Ponieważ liczba równań i liczba niewiadomych mogą się różnić, możliwe są trzy przypadki:
- System jest niespójny, tj. zbiór wszystkich rozwiązań jest pusty. Dość rzadki przypadek, który można łatwo wykryć niezależnie od metody zastosowanej do rozwiązania systemu.
- System jest spójny i zdeterminowany, tj. ma dokładnie jedno rozwiązanie. Wersja klasyczna, dobrze znana ze szkoły.
- System jest spójny i nieokreślony, tj. ma nieskończenie wiele rozwiązań. To najtrudniejsza opcja. Nie wystarczy wskazać, że „system ma nieskończony zbiór rozwiązań” – trzeba opisać, jak ten zbiór jest zbudowany.
Zmienną x i nazywamy dozwoloną, jeśli występuje tylko w jednym równaniu układu i ma współczynnik równy 1. Innymi słowy, w innych równaniach współczynnik zmiennej x i musi być równy zero.
Jeśli w każdym równaniu wybierzemy jedną dozwoloną zmienną, otrzymamy zbiór dozwolonych zmiennych dla całego układu równań. Sam system napisany w tej formie będzie również nazywany rozwiązanym. Ogólnie rzecz biorąc, jeden i ten sam oryginalny system można sprowadzić do różnych dozwolonych, ale na razie się tym nie przejmujemy. Oto przykłady dozwolonych systemów:
Obydwa systemy są rozwiązywane w odniesieniu do zmiennych x 1 , x 3 i x 4 . Jednakże z takim samym sukcesem można argumentować, że drugi system jest rozwiązany w odniesieniu do x 1, x 3 i x 5. Wystarczy przepisać ostatnie równanie do postaci x 5 = x 4.
Rozważmy teraz bardziej ogólny przypadek. Miejmy w sumie k zmiennych, z których r jest dozwolone. Możliwe są wówczas dwa przypadki:
- Liczba dozwolonych zmiennych r jest równa całkowitej liczbie zmiennych k: r = k. Otrzymujemy układ k równań, w którym r = k dopuszczalnych zmiennych. Taki system jest wspólny i określony, ponieważ x 1 = b 1, x 2 = b 2, ..., x k = b k;
- Liczba dozwolonych zmiennych r jest mniejsza niż całkowita liczba zmiennych k: r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Zatem w powyższych systemach zmienne x 2, x 5, x 6 (dla pierwszego systemu) i x 2, x 5 (dla drugiego) są dowolne. Przypadek, w którym istnieją zmienne wolne, lepiej jest sformułować jako twierdzenie:
Uwaga: to bardzo ważny punkt! W zależności od tego, jak napiszesz wynikowy system, ta sama zmienna może być dozwolona lub bezpłatna. Większość nauczycieli matematyki na poziomie wyższym zaleca zapisywanie zmiennych w porządku leksykograficznym, tj. indeks rosnący. Nie masz jednak obowiązku stosowania się do tej porady.
Twierdzenie. Jeżeli w układzie n równań dopuszczalne są zmienne x 1, x 2, ..., x r oraz x r + 1, x r + 2, ..., x k są wolne, to:
- Jeśli ustalimy wartości zmiennych wolnych (x r + 1 = t r + 1, x r + 2 = t r + 2, ..., x k = t k), a następnie znajdziemy wartości x 1, x 2, ..., x r, otrzymujemy jedną z decyzji.
- Jeśli w dwóch rozwiązaniach wartości zmiennych wolnych są zbieżne, to wartości zmiennych dozwolonych również są zbieżne, tj. rozwiązania są równe.
Jakie jest znaczenie tego twierdzenia? Aby otrzymać wszystkie rozwiązania rozwiązanego układu równań wystarczy wyizolować zmienne swobodne. Następnie przypisując różne wartości wolnym zmiennym otrzymamy gotowe rozwiązania. To wszystko - w ten sposób można uzyskać wszystkie rozwiązania systemu. Nie ma innych rozwiązań.
Wniosek: rozwiązany układ równań jest zawsze spójny. Jeśli liczba równań w rozwiązanym układzie jest równa liczbie zmiennych, układ będzie określony, jeśli jest mniejszy, będzie nieokreślony.
I wszystko byłoby dobrze, ale pojawia się pytanie: jak uzyskać rozwiązany z pierwotnego układu równań? Do tego istnieje
Definicja. System M równania z n niewiadomymi w postaci ogólnej zapisuje się w następujący sposób:
Gdzie ij są współczynnikami i b ja- stały.
Rozwiązania układu są N liczby, które po podstawieniu do systemu zamieniają każde z jego równań w tożsamość.
Definicja. Jeśli układ ma co najmniej jedno rozwiązanie, nazywa się go połączeniem. Jeśli system nie ma jednego rozwiązania, nazywa się go niespójnym.
Definicja. Układ nazywamy wyznaczonym, jeśli ma tylko jedno rozwiązanie, i nieokreślonym, jeśli ma więcej niż jedno.
Definicja. Dla układu równań liniowych macierz
A = 
nazywa się macierzą układu i macierzą
A * = 
nazywaną rozszerzoną macierzą układu
Definicja. Jeśli b 1 , b 2 , …,b m = 0, wówczas układ nazywa się jednorodnym. Komentarz. System jednorodny jest zawsze spójny, ponieważ zawsze ma rozwiązanie zerowe.
Elementarne transformacje systemów.
1. Dodanie do obu stron jednego równania odpowiednich części drugiego, pomnożonych przez tę samą liczbę, różną od zera.
2. Przekształcanie równań.
3. Usunięcie z układu równań, które są tożsamościami dla wszystkich X.
Wzory Cramera.
Metodę tę można zastosować także tylko w przypadku układów równań liniowych, gdzie liczba zmiennych pokrywa się z liczbą równań.
Twierdzenie. Układ n równań z n niewiadomymi
jeżeli wyznacznik macierzy układu nie jest równy zero, to układ ma jednoznaczne rozwiązanie i rozwiązanie to wyznacza się za pomocą wzorów: x ja = Gdzie D = det A, A D ja jest wyznacznikiem macierzy otrzymanej z macierzy układu poprzez zastąpienie kolumny I kolumna wolnych członków b ja.
D ja = 
Przykład. Znajdź rozwiązanie układu równań: 
re = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
re 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.
re 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
re 3 = = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
Notatka 1. Jeśli układ jest jednorodny, tj. b ja = 0, to dla D¹0 układ ma jednoznaczne rozwiązanie zerowe x 1 = x 2 = … = x n = 0.
Uwaga 2. Na D=0 układ ma nieskończoną liczbę rozwiązań.
Metoda macierzy odwrotnej.
Metodę macierzową stosuje się do rozwiązywania układów równań, w których liczba równań jest równa liczbie niewiadomych.
Niech będzie dany układ równań: Stwórzmy macierze:
A= 
- macierz współczynników dla zmiennych lub macierz układu;
B = - macierz – kolumna wolnych terminów;
X = - macierz – kolumna niewiadomych.
Można wówczas zapisać układ równań: A×X = B. Pomnóżmy obie strony równości od lewej przez A -1: A -1 ×A×X = A -1 ×B, ponieważ A-1×A = E, To E×X = A -1×B, wówczas obowiązuje następujący wzór:
X = A-1×B
Dlatego, aby zastosować tę metodę, konieczne jest znalezienie odwrotna macierz.
Przykład. Rozwiąż układ równań:
X = , B = , A =
Znajdźmy macierz odwrotną A -1.
D = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ istnieje macierz odwrotna.
M 11 = ; M 21 = ; M 31 = ;
M 12 = M 22 = M 32 =
M 13 = M 23 = M 33 =
A-1 = 
;
Sprawdźmy:
A×A -1 = 
=E.
Znalezienie macierzy X.
X = = A -1 B = × = 
.
Otrzymaliśmy rozwiązania systemowe: x = 1; y = 2; z = 3.
4. Metoda Gaussa.
Niech będzie dany system M równania liniowe z N nieznany:
Zakładając, że współczynnik w systemie A 11 jest różne od zera (jeśli tak nie jest, wówczas równanie z niezerowym współczynnikiem przy X 1). Przekształcamy układ w następujący sposób: pierwsze równanie pozostawiamy bez zmian, a niewiadome wykluczamy ze wszystkich pozostałych równań X 1 stosując równoważne przekształcenia w sposób opisany powyżej.
W powstałym układzie
,
zakładając, że (co zawsze można uzyskać przez przestawienie równań lub wyrazów w obrębie równań) dwa pierwsze równania układu pozostawiamy bez zmian, a z pozostałych równań, korzystając z drugiego równania, eliminujemy niewiadome za pomocą przekształceń elementarnych X 2. W nowo otrzymanym systemie
pod warunkiem, że trzy pierwsze równania pozostawimy bez zmian, a ze wszystkich pozostałych, korzystając z trzeciego równania, wyeliminujemy niewiadomą poprzez elementarne przekształcenia X 3 .
Proces ten trwa aż do wystąpienia jednego z trzech możliwych przypadków:
1) jeśli w rezultacie otrzymamy układ, którego jedno z równań ma zerowe współczynniki dla wszystkich niewiadomych i niezerowy człon wolny, to pierwotny układ jest niespójny;
2) jeżeli w wyniku przekształceń otrzymamy układ z trójkątną macierzą współczynników, to układ ten jest spójny i określony;
3) jeżeli otrzymamy schodkowy układ współczynników (i nie jest spełniony warunek z pkt. 1), to układ ten jest spójny i nieokreślony.
Rozważmy system kwadratowy :
(1)
Układ ten ma współczynnik A 11 jest różne od zera. Gdyby ten warunek nie był spełniony, to aby go uzyskać, należałoby przestawić równania, stawiając na pierwszym miejscu równanie, którego współczynnik wynosi X 1 nie jest równe zero.
Przeprowadzimy następujące przekształcenia systemowe:
1) ponieważ A 11 ¹0, pierwsze równanie pozostawiamy bez zmian;
2) zamiast drugiego równania zapisujemy równanie otrzymane, jeśli od drugiego równania odejmiemy pierwsze pomnożone przez 4;
3) zamiast trzeciego równania zapisujemy różnicę między trzecim a pierwszym równaniem pomnożoną przez 3;
4) zamiast czwartego równania zapisujemy różnicę między czwartym a pierwszym, pomnożoną przez 5.
Powstały nowy układ jest równoważny pierwotnemu i ma zerowe współczynniki we wszystkich równaniach z wyjątkiem pierwszego. X 1 (taki był cel przekształceń 1 – 4): 
(2)
W przypadku powyższej transformacji i wszystkich dalszych transformacji nie należy całkowicie przepisywać całego systemu, jak to właśnie zrobiono. Oryginalny system można przedstawić w postaci macierzy
. (3)
Nazywa się macierz (3). rozszerzona matryca dla pierwotnego układu równań. Jeśli usuniemy kolumnę wolnych terminów z rozszerzonej macierzy, otrzymamy macierz współczynników systemu, co czasami jest nazywane po prostu macierz układu.
Układ (2) odpowiada rozszerzonej macierzy
.
Przekształćmy tę macierz w następujący sposób:
1) pierwsze dwie linie pozostawimy bez zmian, ponieważ element A 22 nie jest zerem;
2) zamiast trzeciej linii wpisujemy różnicę między drugą linią a podwójną trzecią linią;
3) zastąp czwartą linię różnicą między drugą linią podwojoną a czwartą linią pomnożoną przez 5.
Wynikiem jest macierz odpowiadająca układowi, którego niewiadoma X Liczba 1 jest wykluczona ze wszystkich równań z wyjątkiem pierwszego i nieznanej X 2 - ze wszystkich równań oprócz pierwszego i drugiego:
.
Teraz wykluczmy nieznane X 3 z czwartego równania. W tym celu przekształcamy ostatnią macierz w następujący sposób:
1) pierwsze trzy linie pozostawimy bez zmian, ponieważ A 33¹0;
2) zastąp czwartą linię różnicą między trzecią pomnożoną przez 39 a czwartą linią: 
.
Otrzymana macierz odpowiada systemowi
. (4)
Z ostatniego równania tego układu otrzymujemy X 4 = 2. Podstawiając tę wartość do trzeciego równania, otrzymujemy X 3 = 3. Z drugiego równania wynika to X 2 = 1, a od pierwszego - X 1 = –1. Jest oczywiste, że powstałe rozwiązanie jest unikalne (ponieważ wartość jest określana w jedyny sposób X 4 wtedy X 3 itd.).
Definicja: Nazwijmy macierz kwadratową, która ma niezerowe liczby na głównej przekątnej i zera poniżej głównej przekątnej, macierz trójkątna.
Macierz współczynników układu (4) jest macierzą trójkątną.
Komentarz: Jeżeli za pomocą przekształceń elementarnych macierz współczynników układu kwadratowego można sprowadzić do macierzy trójkątnej, to układ ten jest spójny i określony.
Spójrzmy na inny przykład: 
. (5)
Przeprowadźmy następujące przekształcenia rozszerzonej macierzy układu:
1) pozostawić pierwszą linię bez zmian;
2) zamiast drugiej linii wpisz różnicę między drugą linią a podwójną linią pierwszą;
3) zamiast trzeciej linii wpisujemy różnicę między trzecią linią a potrójną pierwszą linią;
4) zastąpić czwarty wiersz różnicą między czwartym a pierwszym wierszem;
5) zamień piątą linię na różnicę piątej linii i podwoj pierwszą.
W wyniku przekształceń otrzymujemy macierz
.
Pozostawiając dwa pierwsze wiersze tej macierzy bez zmian, poprzez elementarne przekształcenia sprowadzamy ją do postaci:
.
Jeśli teraz, stosując metodę Gaussa, zwaną także metodą sekwencyjnej eliminacji niewiadomych, za pomocą trzeciej linii doprowadzimy współczynniki przy X 3 w czwartym i piątym rzędzie, następnie po podzieleniu wszystkich elementów drugiego rzędu przez 5 i podzieleniu wszystkich elementów trzeciego rzędu przez 2 otrzymujemy macierz
.
Każdy z dwóch ostatnich wierszy tej macierzy odpowiada równaniu 0 X 1 +0X 2 +0X 3 +0X 4 +0X 5 = 0. To równanie spełnia dowolny zbiór liczb X 1 ,X 2, ¼, X 5 i należy je usunąć z systemu. Zatem układ z otrzymaną właśnie rozszerzoną macierzą jest równoważny układowi z rozszerzoną macierzą postaci
. (6)
Ostatni wiersz tej macierzy odpowiada równaniu
X 3 – 2X 4 + 3X 5 = –4. Jeśli nieznany X 4 i X 5 podaj dowolne wartości: X 4 = C 1; X 5 = C 2, to z ostatniego równania układu odpowiadającego macierzy (6) otrzymujemy X 3 = –4 + 2C 1 – 3C 2. Zastępowanie wyrażeń X 3 ,X 4 i X 5 do drugiego równania tego samego układu, otrzymujemy X 2 = –3 + 2C 1 – 2C 2. Teraz z pierwszego równania, które możemy otrzymać X 1 = 4 – C 1+ C 2. Ostateczne rozwiązanie układu przedstawiono w formie 
.
Rozważmy macierz prostokątną A, którego liczba kolumn M więcej niż liczba linii N. Taka matryca A zadzwońmy wkroczył.
Jest oczywiste, że macierz (6) jest macierzą schodkową.
Jeżeli przy zastosowaniu równoważnych przekształceń do układu równań co najmniej jedno równanie zostanie sprowadzone do postaci
0X 1 + 0X 2 + ¼0 x rz = bj (bj ¹ 0),
wówczas system jest niezgodny lub sprzeczny, ponieważ nie ma jednego zestawu liczb X 1 , X 2, ¼, x rz nie spełnia tego równania.
Jeżeli przy transformacji rozszerzonej macierzy układu macierz współczynników sprowadzi się do postaci schodkowej i układ nie okaże się niespójny, to układ jest spójny i nieokreślony, czyli ma nieskończenie wiele rozwiązań.
W tym drugim systemie wszystkie rozwiązania można uzyskać poprzez przypisanie parametrom określonych wartości liczbowych C 1 I C 2.
Definicja: Te zmienne, których współczynniki znajdują się na głównej przekątnej macierzy schodkowej (oznacza to, że współczynniki te są różne od zera) nazywane są o główny. W przykładzie omówionym powyżej są to niewiadome X 1 , X 2 , X 3. Pozostałe zmienne są wywoływane nie-rdzeniowe. W powyższym przykładzie są to zmienne X 4 i X 5. Zmienne inne niż podstawowe mogą mieć przypisane dowolne wartości lub być wyrażone poprzez parametry, tak jak to miało miejsce w ostatnim przykładzie.
Zmienne podstawowe są jednoznacznie wyrażane poprzez zmienne inne niż podstawowe.
Definicja: Jeśli zmiennym innym niż główne zostaną podane określone wartości liczbowe i wyrażone zostaną za ich pośrednictwem zmienne główne, wówczas powstałe rozwiązanie nazywa się rozwiązanie prywatne.
Definicja: Jeśli zmienne niepodstawowe wyrażone są w kategoriach parametrów, wówczas uzyskuje się rozwiązanie, które nazywa się rozwiązanie ogólne.
Definicja: Jeżeli wszystkim zmiennym drugorzędnym przypisano wartości zerowe, wywoływane jest powstałe rozwiązanie podstawowy.
Komentarz: Ten sam system można czasami sprowadzić do różnych zestawów podstawowych zmiennych. Można więc na przykład zamienić trzecią i czwartą kolumnę w macierzy (6). Wtedy będą główne zmienne X 1 , X 2 ,X 4 i inne niż główne - X 3 i X 5 .
Definicja: Jeżeli przy użyciu różnych metod znajdowania rozwiązania tego samego układu otrzyma się dwa różne zbiory zmiennych podstawowych, to zbiory te koniecznie zawierają tę samą liczbę zmiennych, tzw. ranga systemu.
Rozważmy inny układ, który ma nieskończenie wiele rozwiązań: 
.
Przekształćmy rozszerzoną macierz układu metodą Gaussa:
.
Jak widać nie otrzymaliśmy macierzy schodkowej, ale ostatnią macierz można przekształcić zamieniając trzecią i czwartą kolumnę: 
.
Ta macierz jest już schodkowa. Odpowiedni system ma dwie niepodstawowe zmienne - X 3 , X 5 i trzy główne - X 1 , X 2 , X 4. Rozwiązanie oryginalnego układu przedstawiono w następującej postaci:
Oto przykład układu, który nie ma rozwiązania:
.
Przekształćmy macierz układu metodą Gaussa:
.
Ostatni wiersz ostatniej macierzy odpowiada nierozwiązywalnemu równaniu 0x 1 + 0x 2 + 0x 3 = 1. W rezultacie pierwotny system jest niespójny.
Wykład nr 3.
Temat: Wektory. Skalar, wektor i iloczyn mieszany wektorów
1. Pojęcie wektora. Kolinearność, ortogonalność i współpłaszczyznowość wektorów.
2. Operacje liniowe na wektorach.
3. Iloczyn skalarny wektorów i jego zastosowanie
4. Iloczyn krzyżowy wektorów i jego zastosowanie
5. Iloczyn mieszany wektorów i jego zastosowanie
1. Pojęcie wektora.Kolinarność, ortogonalność i współpłaszczyznowość wektorów.
| |
Przeznaczenie: , ,
Definicja: Długość lub moduł wektora wektorowego jest liczbą równą długości odcinka AB reprezentującego wektor.
Definicja: Wektor nazywa się zerem, jeśli początek i koniec wektora pokrywają się.
Definicja: Wektor o długości jednostkowej nazywa się jednostką. Definicja: Wektory nazywane są współliniowymi, jeśli leżą na tej samej prostej lub na liniach równoległych ( || ).
Komentarz:
1.Wektory współliniowe mogą być skierowane identycznie lub przeciwnie.
2. Uważa się, że wektor zerowy jest współliniowy z dowolnym wektorem.
Definicja: Mówi się, że dwa wektory są równe, jeśli są współliniowe,
mają te same kierunki i tę samą długość ( = )
Jednak w praktyce powszechne są jeszcze dwa przypadki:
– Układ jest niespójny (nie ma rozwiązań);
– Układ jest spójny i ma nieskończenie wiele rozwiązań.
Notatka : Termin „spójność” oznacza, że system ma przynajmniej pewne rozwiązanie. W przypadku wielu problemów należy najpierw sprawdzić system pod kątem kompatybilności, jak to zrobić, zobacz artykuł na temat rząd macierzy.
W przypadku tych układów stosuje się najbardziej uniwersalną ze wszystkich metod rozwiązań - Metoda Gaussa. W rzeczywistości metoda „szkolna” również doprowadzi do odpowiedzi, ale w wyższej matematyce zwyczajowo stosuje się metodę Gaussa sekwencyjnej eliminacji niewiadomych. Ci, którzy nie są zaznajomieni z algorytmem metody Gaussa, powinni najpierw przestudiować lekcję Metoda Gaussa dla manekinów.
Same transformacje macierzy elementarnych są dokładnie takie same, różnica będzie polegać na zakończeniu rozwiązania. Najpierw spójrzmy na kilka przykładów, gdy układ nie ma rozwiązań (niespójny).
Przykład 1
Co od razu rzuca się w oczy w tym systemie? Liczba równań jest mniejsza niż liczba zmiennych. Jeśli liczba równań jest mniejsza niż liczba zmiennych, to od razu możemy powiedzieć, że układ jest albo niespójny, albo ma nieskończenie wiele rozwiązań. I jedyne, co pozostaje, to się dowiedzieć.
Początek rozwiązania jest zupełnie zwyczajny – zapisujemy rozszerzoną macierz układu i za pomocą elementarnych przekształceń doprowadzamy ją do postaci krokowej:
(1) W lewym górnym kroku musimy uzyskać +1 lub –1. W pierwszej kolumnie nie ma takich liczb, więc przestawianie wierszy nic nie da. Jednostka będzie musiała się zorganizować sama, a można to zrobić na kilka sposobów. Zrobiłem tak: Do pierwszej linii dodajemy trzecią linię pomnożoną przez -1.
(2) Teraz w pierwszej kolumnie otrzymujemy dwa zera. Do drugiej linii dodajemy pierwszą linię pomnożoną przez 3. Do trzeciej linii dodajemy pierwszą linię pomnożoną przez 5.
(3) Po zakończeniu transformacji zawsze warto sprawdzić, czy możliwe jest uproszczenie powstałych ciągów znaków? Móc. Drugą linię dzielimy przez 2, uzyskując jednocześnie wymagane –1 w drugim kroku. Podziel trzecią linię przez –3.
(4) Dodaj drugą linię do trzeciej linii.
Chyba każdy zauważył złą linię wynikającą z elementarnych przekształceń: 
. Jasne jest, że tak nie może być. Rzeczywiście, przepiszemy otrzymaną macierz 
wracając do układu równań liniowych: 
Jeżeli w wyniku przekształceń elementarnych otrzymamy ciąg znaków w postaci, w której jest liczba różna od zera, to układ jest niespójny (nie ma rozwiązań).
Jak zapisać zakończenie zadania? Narysujmy białą kredą: „w wyniku przekształceń elementarnych otrzymujemy ciąg znaków w postaci , gdzie ” i podajemy odpowiedź: układ nie ma rozwiązań (niespójny).
Jeśli zgodnie z warunkiem wymagane jest BADANIE systemu pod kątem kompatybilności, konieczne jest sformalizowanie rozwiązania w bardziej solidny sposób, korzystając z koncepcji rząd macierzy i twierdzenie Kroneckera-Capelliego.
Należy pamiętać, że nie ma tu odwrócenia algorytmu Gaussa – nie ma rozwiązań i po prostu nie ma czego szukać.
Przykład 2
Rozwiązać układ równań liniowych 
To jest przykład, który możesz rozwiązać samodzielnie. Pełne rozwiązanie i odpowiedź na końcu lekcji. Przypominam jeszcze raz, że Twoje rozwiązanie może różnić się od mojego, algorytm Gaussa nie charakteryzuje się dużą „sztywnością”.
Kolejna cecha techniczna rozwiązania: można zatrzymać przekształcenia elementarne Natychmiast, jak tylko pojawi się linia typu , gdzie . Rozważmy przykład warunkowy: załóżmy, że po pierwszej transformacji otrzymana zostanie macierz 
. Macierz nie została jeszcze zredukowana do postaci schodkowej, ale nie ma potrzeby dalszych elementarnych przekształceń, gdyż pojawiła się linia postaci, gdzie . Należy od razu odpowiedzieć, że system jest niekompatybilny.
Kiedy układ równań liniowych nie ma rozwiązań, jest to niemal prezent, ponieważ uzyskuje się krótkie rozwiązanie, czasem dosłownie w 2-3 krokach.
Ale wszystko na tym świecie jest zrównoważone, a problem, w którym układ ma nieskończenie wiele rozwiązań, jest po prostu dłuższy.
Przykład 3
Rozwiązać układ równań liniowych 
Istnieją 4 równania i 4 niewiadome, więc układ może mieć jedno rozwiązanie, nie mieć rozwiązań, lub mieć nieskończenie wiele rozwiązań. Tak czy inaczej, metoda Gaussa w każdym razie doprowadzi nas do odpowiedzi. Na tym polega jego wszechstronność.
Początek znowu standardowy. Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej: 
To wszystko, a ty się bałeś.
(1) Należy pamiętać, że wszystkie liczby w pierwszej kolumnie są podzielne przez 2, więc 2 jest w porządku w lewym górnym kroku. Do drugiej linii dodajemy pierwszą linię pomnożoną przez –4. Do trzeciej linii dodajemy pierwszą linię pomnożoną przez –2. Do czwartej linii dodajemy pierwszą linię pomnożoną przez –1.
Uwaga! Wielu może skusić czwarta linijka odejmować Pierwsza linia. Można to zrobić, ale nie jest to konieczne, doświadczenie pokazuje, że prawdopodobieństwo błędu w obliczeniach wzrasta kilkakrotnie. Po prostu dodaj: Do czwartej linii dodaj pierwszą linię pomnożoną przez –1 – Dokładnie!
(2) Trzy ostatnie linie są proporcjonalne, dwie z nich można usunąć.
Tutaj znowu musimy się pokazać zwiększona uwaga, ale czy linie są rzeczywiście proporcjonalne? Dla bezpieczeństwa (zwłaszcza w przypadku czajnika) dobrze byłoby pomnożyć drugą linię przez –1, a czwartą linię podzielić przez 2, w wyniku czego otrzymamy trzy identyczne linie. I dopiero potem usuń dwa z nich.
W wyniku elementarnych przekształceń rozszerzona macierz układu sprowadza się do postaci krokowej: 
Pisząc zadanie w zeszycie, zaleca się robienie tych samych notatek ołówkiem dla przejrzystości.
Przepiszmy odpowiedni układ równań: 
Nie ma tu zapachu „zwykłego” pojedynczego rozwiązania systemu. Nie ma też złej linii. Oznacza to, że jest to trzeci pozostały przypadek – układ ma nieskończenie wiele rozwiązań. Czasami zgodnie z warunkiem konieczne jest zbadanie kompatybilności systemu (czyli udowodnienie, że rozwiązanie w ogóle istnieje), możesz o tym przeczytać w ostatnim akapicie artykułu Jak znaleźć rząd macierzy? Ale na razie przejdźmy do podstaw:
Nieskończony zbiór rozwiązań układu zapisuje się w skrócie w postaci tzw ogólne rozwiązanie układu .
Rozwiązanie ogólne układu znajdujemy za pomocą odwrotności metody Gaussa.
Najpierw musimy zdefiniować, jakie mamy zmienne podstawowy i jakie zmienne bezpłatny. Nie musisz zawracać sobie głowy terminami algebry liniowej, pamiętaj tylko, że takie istnieją podstawowe zmienne I wolne zmienne.
Zmienne podstawowe zawsze „siedzą” ściśle na stopniach macierzy.
W tym przykładzie podstawowymi zmiennymi są i
Wolne zmienne są wszystkim pozostały zmienne, które nie otrzymały kroku. W naszym przypadku są dwa z nich: – zmienne wolne.
Teraz potrzebujesz Wszystko podstawowe zmienne wyrazić tylko przez wolne zmienne.
Odwrotność algorytmu Gaussa tradycyjnie działa od dołu do góry.
Z drugiego równania układu wyrażamy zmienną podstawową:
Spójrzmy teraz na pierwsze równanie: 
. Najpierw podstawiamy do niego znalezione wyrażenie: 
Pozostaje wyrazić zmienną podstawową w kategoriach zmiennych wolnych: 
W końcu mamy to, czego potrzebowaliśmy – Wszystko wyrażane są podstawowe zmienne ( i ). tylko przez wolne zmienne: 
Właściwie ogólne rozwiązanie jest gotowe: 
Jak poprawnie napisać rozwiązanie ogólne?
Zmienne swobodne wpisuje się do rozwiązania ogólnego „same” i ściśle na swoich miejscach. W takim przypadku zmienne wolne należy zapisać na drugiej i czwartej pozycji: 
.
Wynikowe wyrażenia dla podstawowych zmiennych 
i oczywiście należy zapisać na pierwszej i trzeciej pozycji: 
Podawanie wolnych zmiennych dowolne wartości, możesz znaleźć nieskończenie wiele rozwiązania prywatne. Najpopularniejszymi wartościami są zera, gdyż dane rozwiązanie jest najłatwiejsze do uzyskania. Podstawmy do rozwiązania ogólnego: 
– rozwiązanie prywatne.
Kolejną słodką parą są jedynki, podstawmy je do ogólnego rozwiązania: 
– kolejne rozwiązanie prywatne.
Łatwo zobaczyć, że układ równań ma nieskończenie wiele rozwiązań(ponieważ możemy podać darmowe zmienne każdy wartości)
Każdy dane rozwiązanie musi spełniać do każdego równanie układu. Jest to podstawa do „szybkiego” sprawdzenia poprawności rozwiązania. Weźmy na przykład konkretne rozwiązanie i podstawmy je po lewej stronie każdego równania pierwotnego układu: 
Wszystko musi się zgadzać. W przypadku każdego konkretnego rozwiązania, które otrzymasz, wszystko powinno się zgadzać.
Ale ściśle rzecz biorąc, sprawdzanie konkretnego rozwiązania czasami jest zwodnicze, tj. jakieś szczególne rozwiązanie może spełniać każde równanie układu, ale samo rozwiązanie ogólne jest w rzeczywistości znajdowane niepoprawnie.
Dlatego weryfikacja rozwiązania ogólnego jest dokładniejsza i bardziej wiarygodna. Jak sprawdzić wynikowe rozwiązanie ogólne 
?
Nie jest to trudne, ale dość żmudne. Musimy przyjąć wyrażenia podstawowy w tym przypadku zmienne 
i , i podstaw je po lewej stronie każdego równania układu.
Po lewej stronie pierwszego równania układu: 
Po lewej stronie drugiego równania układu: 
Otrzymuje się prawą stronę pierwotnego równania.
Przykład 4
Rozwiązać układ metodą Gaussa. Znajdź rozwiązanie ogólne i dwa szczegółowe. Sprawdź rozwiązanie ogólne. 
To jest przykład, który możesz rozwiązać samodzielnie. Tutaj, nawiasem mówiąc, znowu liczba równań jest mniejsza niż liczba niewiadomych, co oznacza od razu jasne, że układ będzie albo niespójny, albo będzie miał nieskończoną liczbę rozwiązań. Co jest ważne w samym procesie decyzyjnym? Uwaga i jeszcze raz uwaga. Pełne rozwiązanie i odpowiedź na końcu lekcji.
I jeszcze kilka przykładów wzmocnienia materiału
Przykład 5
Rozwiązać układ równań liniowych. Jeżeli układ ma nieskończenie wiele rozwiązań, znajdź dwa rozwiązania szczególne i sprawdź rozwiązanie ogólne 
Rozwiązanie: Zapiszmy rozszerzoną macierz układu i za pomocą elementarnych przekształceń sprowadźmy ją do postaci krokowej: 
(1) Dodaj pierwszą linię do drugiej linii. Do trzeciej linii dodajemy pierwszą linię pomnożoną przez 2. Do czwartej linii dodajemy pierwszą linię pomnożoną przez 3.
(2) Do trzeciej linii dodajemy drugą linię pomnożoną przez –5. Do czwartej linii dodajemy drugą linię pomnożoną przez –7.
(3) Trzecia i czwarta linia są takie same, usuwamy jedną z nich.
To taka piękność: 
Na stopniach znajdują się zmienne podstawowe, zatem - zmienne podstawowe.
Jest tylko jedna wolna zmienna, która nie dostała kroku:
Odwracać:
Wyraźmy podstawowe zmienne poprzez zmienną wolną:
Z trzeciego równania: 
Rozważmy drugie równanie i podstawmy do niego znalezione wyrażenie: 
Rozważmy pierwsze równanie i podstawmy znalezione wyrażenia i do niego: 
Tak, kalkulator obliczający ułamki zwykłe jest nadal wygodny.
Zatem ogólne rozwiązanie jest następujące: 
Jeszcze raz, jak to się skończyło? Zmienna wolna zajmuje samotne, czwarte miejsce. Powstałe wyrażenia dla zmiennych podstawowych również zajęły swoje miejsca porządkowe.
Sprawdźmy od razu rozwiązanie ogólne. Praca jest dla czarnych, ale ja już ją zrobiłem, więc łapcie =)
Podstawiamy trzech bohaterów , , po lewej stronie każdego równania układu:
Otrzymuje się odpowiednie prawe strony równań, a zatem rozwiązanie ogólne zostaje znalezione poprawnie.
Teraz ze znalezionego ogólnego rozwiązania 
otrzymujemy dwa konkretne rozwiązania. Jedyną wolną zmienną jest tutaj szef kuchni. Nie ma potrzeby zawracać sobie głowy.
Niech tak będzie 
– rozwiązanie prywatne.
Niech będzie zatem kolejnym konkretnym rozwiązaniem.
Odpowiedź: Wspólna decyzja: 
, rozwiązania prywatne: 
, .
Nie powinienem był pamiętać o czarnych... ...bo do głowy przychodziły mi najróżniejsze sadystyczne motywy i przypomniał mi się słynny photoshop, w którym członkowie Ku Klux Klanu w białych szatach biegają po boisku za czarnym piłkarzem. Siedzę i cicho się uśmiecham. Wiesz, jakie to rozpraszające...
Dużo matematyki jest szkodliwe, więc podobny końcowy przykład rozwiązania tego samodzielnie.
Przykład 6
Znajdź rozwiązanie ogólne układu równań liniowych. 
Sprawdziłem już ogólne rozwiązanie, odpowiedzi można zaufać. Twoje rozwiązanie może różnić się od mojego, najważniejsze jest to, że ogólne rozwiązania są zbieżne.
Prawdopodobnie wiele osób zauważyło nieprzyjemny moment w rozwiązaniach: bardzo często podczas odwrotnego przebiegu metody Gaussa musieliśmy majstrować przy zwykłych ułamkach. W praktyce rzeczywiście tak jest; przypadki, w których nie ma ułamków, są znacznie mniej powszechne. Bądź przygotowany mentalnie i, co najważniejsze, technicznie.
Zatrzymam się nad niektórymi cechami rozwiązania, których nie znaleziono w rozwiązanych przykładach.
Ogólne rozwiązanie układu może czasami zawierać stałą (lub stałe), na przykład: . Tutaj jedna z podstawowych zmiennych jest równa liczbie stałej: . Nie ma w tym nic egzotycznego, zdarza się. Oczywiście w tym przypadku każde konkretne rozwiązanie będzie zawierało piątkę na pierwszej pozycji.
Rzadko, ale są systemy, w których liczba równań jest większa niż liczba zmiennych. Metoda Gaussa sprawdza się w najcięższych warunkach, należy spokojnie sprowadzić rozszerzoną macierz układu do postaci krokowej stosując standardowy algorytm. Taki system może być niespójny, może mieć nieskończenie wiele rozwiązań i, co dziwne, może mieć jedno rozwiązanie.
Przykład 1. Znajdź rozwiązanie ogólne i rozwiązanie szczególne układuRozwiązanie Robimy to za pomocą kalkulatora. Zapiszmy macierze rozszerzone i główne: 
Macierz główną A oddzielono linią przerywaną.Nieznane układy zapisujemy na górze, pamiętając o możliwości przestawienia wyrazów w równaniach układu. Wyznaczając rangę macierzy rozszerzonej, jednocześnie znajdujemy rangę macierzy głównej. W macierzy B pierwsza i druga kolumna są proporcjonalne. Z dwóch kolumn proporcjonalnych tylko jedna może wpaść w moll podstawowy, zatem przesuńmy np. pierwszą kolumnę poza linię przerywaną z przeciwległym znakiem. Dla układu oznacza to przeniesienie wyrazów z x 1 na prawą stronę równań. 
Sprowadźmy macierz do postaci trójkątnej. Będziemy pracować tylko z wierszami, gdyż pomnożenie wiersza macierzy przez liczbę różną od zera i dodanie go do innego wiersza dla układu oznacza pomnożenie równania przez tę samą liczbę i dodanie go przez inne równanie, co nie zmienia rozwiązania układu system. Pracujemy z pierwszym wierszem: pomnóż pierwszy wiersz macierzy przez (-3) i dodaj kolejno do drugiego i trzeciego wiersza. Następnie pomnóż pierwszą linię przez (-2) i dodaj do czwartej. 
Druga i trzecia linia są proporcjonalne, dlatego jedną z nich, na przykład drugą, można przekreślić. Jest to równoznaczne z przekreśleniem drugiego równania układu, ponieważ jest konsekwencją trzeciego. 
Teraz pracujemy z drugą linią: pomnóż ją przez (-1) i dodaj do trzeciej. 
Moll zakreślony linią przerywaną ma najwyższy rząd (z możliwych minorów) i jest niezerowy (jest równy iloczynowi elementów na głównej przekątnej), a ten minor należy zarówno do macierzy głównej, jak i rozszerzonej, zatem rangA = rangB = 3.
Drobny 
jest podstawowe. Zawiera współczynniki dla niewiadomych x 2 , x 3 , x 4 , co oznacza, że niewiadome x 2 , x 3 , x 4 są zależne, a x 1 , x 5 są wolne.
Przekształćmy macierz, pozostawiając po lewej stronie jedynie bazę mniejszą (co odpowiada punktowi 4 powyższego algorytmu rozwiązania). 
Układ o współczynnikach tej macierzy jest równoważny układowi pierwotnemu i ma postać
Stosując metodę eliminacji niewiadomych znajdujemy: 
, ,
Otrzymaliśmy relacje wyrażające zmienne zależne x 2, x 3, x 4 poprzez wolne x 1 i x 5, czyli znaleźliśmy rozwiązanie ogólne: 
Przypisując dowolne wartości wolnym niewiadomym otrzymujemy dowolną liczbę rozwiązań szczegółowych. Znajdźmy dwa konkretne rozwiązania:
1) niech x 1 = x 5 = 0, następnie x 2 = 1, x 3 = -3, x 4 = 3;
2) wstaw x 1 = 1, x 5 = -1, następnie x 2 = 4, x 3 = -7, x 4 = 7.
Znaleziono zatem dwa rozwiązania: (0,1,-3,3,0) – jedno rozwiązanie, (1,4,-7,7,-1) – drugie rozwiązanie.
Przykład 2. Sprawdź kompatybilność, znajdź ogólne i jedno szczególne rozwiązanie dla systemu 
Rozwiązanie. Przekształćmy pierwsze i drugie równanie tak, aby mieć jedynkę w pierwszym równaniu i napiszmy macierz B. 
Zera w czwartej kolumnie otrzymujemy operując na pierwszym wierszu: 
Teraz uzyskujemy zera w trzeciej kolumnie za pomocą drugiej linii: 
Trzecia i czwarta linia są proporcjonalne, więc jedną z nich można przekreślić bez zmiany rangi:
Pomnóż trzecią linię przez (–2) i dodaj do czwartej: 
Widzimy, że szeregi macierzy głównej i rozszerzonej są równe 4, a stopień pokrywa się z liczbą niewiadomych, dlatego układ ma unikalne rozwiązanie:
;
x 4 = 10- 3x 1 – 3x 2 – 2x 3 = 11.
Przykład 3. Sprawdź system pod kątem kompatybilności i znajdź rozwiązanie, jeśli istnieje. 
Rozwiązanie. Tworzymy rozbudowaną matrycę systemu. 
Przekształcamy pierwsze dwa równania tak, aby w lewym górnym rogu znajdowała się liczba 1:
Mnożąc pierwszą linię przez (-1), dodając ją do trzeciej: 
Pomnóż drugą linię przez (-2) i dodaj ją do trzeciej: 
System jest niespójny, ponieważ w macierzy głównej otrzymaliśmy wiersz składający się z zer, który przy znalezieniu rangi jest przekreślany, natomiast w macierzy rozszerzonej pozostaje ostatni wiersz, czyli r B > r A .
Ćwiczenia. Zbadaj ten układ równań pod kątem zgodności i rozwiąż go za pomocą rachunku macierzowego.
Rozwiązanie
Przykład. Udowodnić zgodność układu równań liniowych i rozwiązać go na dwa sposoby: 1) metodą Gaussa; 2) Metoda Cramera. (wpisz odpowiedź w formie: x1,x2,x3)
Rozwiązanie :doc :doc :xls
Odpowiedź: 2,-1,3.
Przykład. Podano układ równań liniowych. Udowodnij jego zgodność. Znajdź rozwiązanie ogólne układu i jedno rozwiązanie szczególne.
Rozwiązanie
Odpowiedź: x 3 = - 1 + x 4 + x 5 ; x 2 = 1 - x 4 ; x 1 = 2 + x 4 - 3x 5
Ćwiczenia. Znajdź rozwiązania ogólne i szczegółowe każdego układu.
Rozwiązanie. Badamy ten układ, korzystając z twierdzenia Kroneckera-Capelliego.
Zapiszmy macierze rozszerzone i główne:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Tutaj macierz A jest wyróżniona pogrubioną czcionką.
Sprowadźmy macierz do postaci trójkątnej. Będziemy pracować tylko z wierszami, gdyż pomnożenie wiersza macierzy przez liczbę różną od zera i dodanie go do innego wiersza dla układu oznacza pomnożenie równania przez tę samą liczbę i dodanie go przez inne równanie, co nie zmienia rozwiązania układu system.
Pomnóżmy pierwszą linię przez (3). Pomnóż drugą linię przez (-1). Dodajmy drugą linię do pierwszej:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Pomnóżmy drugą linię przez (2). Pomnóż trzecią linię przez (-3). Dodajmy trzecią linię do drugiej:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Pomnóż drugą linię przez (-1). Dodajmy drugą linię do pierwszej:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Wybrany moll ma najwyższy rząd (z możliwych minorów) i jest niezerowy (jest równy iloczynowi elementów na odwrotnej przekątnej), a ten minor należy zarówno do macierzy głównej, jak i rozszerzonej, zatem rang( A) = rang(B) = 3 Ponieważ ranga macierzy głównej jest równa rangi macierzy rozszerzonej, to system współpracuje.
Ten drobny element jest podstawowy. Zawiera współczynniki dla niewiadomych x 1 , x 2 , x 3 , co oznacza, że niewiadome x 1 , x 2 , x 3 są zależne (podstawowe), a x 4 , x 5 są wolne.
Przekształćmy macierz, pozostawiając po lewej stronie tylko podstawę mollową.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
27x 3 =
- x 2 + 13x 3 = - 1 + 3x 4 - 6x 5
2x 1 + 3x 2 - 3x 3 = 1 - 3x 4 + 2x 5
Stosując metodę eliminacji niewiadomych znajdujemy:
Otrzymaliśmy relacje wyrażające zmienne zależne x 1 , x 2 , x 3 poprzez wolne x 4 , x 5 , czyli znaleźliśmy wspólna decyzja:
x 3 = 0
x 2 = 1 - 3x 4 + 6x 5
x 1 = - 1 + 3x 4 - 8x 5
niepewny, ponieważ ma więcej niż jedno rozwiązanie.
Ćwiczenia. Rozwiązać układ równań.
Odpowiedź:x 2 = 2 - 1,67x 3 + 0,67x 4
x 1 = 5 - 3,67 x 3 + 0,67 x 4
Przypisując dowolne wartości wolnym niewiadomym otrzymujemy dowolną liczbę rozwiązań szczegółowych. System jest niepewny