Przyjrzyjmy się przykładom dzielenia ułamków dziesiętnych w tym świetle.
Przykład.
Podziel ułamek dziesiętny 1,2 przez ułamek dziesiętny 0,48.
Rozwiązanie.
Odpowiedź:
1,2:0,48=2,5 .
Przykład.
Podziel okresowy ułamek dziesiętny 0.(504) przez ułamek dziesiętny 0,56.
Rozwiązanie.
Zamieńmy okresowy ułamek dziesiętny na ułamek zwykły: . Przeliczamy również końcowy ułamek dziesiętny 0,56 na ułamek zwykły, mamy 0,56 = 56/100. Teraz możemy przejść od dzielenia ułamków dziesiętnych do dzielenia ułamków zwykłych i zakończyć obliczenia: .
Zamieńmy powstały ułamek zwykły na ułamek dziesiętny, dzieląc licznik przez mianownik za pomocą kolumny:
Odpowiedź:
0,(504):0,56=0,(900) .
Zasada dzielenia nieskończonych nieokresowych ułamków dziesiętnych różni się od zasady dzielenia skończonych i okresowych ułamków dziesiętnych, ponieważ nieokresowych ułamków dziesiętnych nie można zamienić na ułamki zwykłe. Dzielenie nieskończonych nieokresowych ułamków dziesiętnych sprowadza się do dzielenia skończonych ułamków dziesiętnych, dla których przeprowadzamy zaokrąglanie liczb do pewnego poziomu. Ponadto, jeśli jedna z liczb, za pomocą których przeprowadza się dzielenie, jest skończonym lub okresowym ułamkiem dziesiętnym, wówczas jest ona również zaokrąglana do tej samej cyfry, co nieokresowy ułamek dziesiętny.
Przykład.
Podziel nieskończony, nieokresowy ułamek dziesiętny 0,779... przez skończony ułamek dziesiętny 1,5602.
Rozwiązanie.
Najpierw musisz zaokrąglić ułamki dziesiętne, aby móc przejść od dzielenia nieskończonych nieokresowych ułamków dziesiętnych do dzielenia skończonych ułamków dziesiętnych. Możemy zaokrąglić do najbliższej setnej: 0,779…≈0,78 i 1,5602≈1,56. Zatem 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100·100/156= 78/156=1/2=0,5 .
Odpowiedź:
0,779…:1,5602≈0,5 .
Dzielenie liczby naturalnej przez ułamek dziesiętny i odwrotnie
Istota podejścia do dzielenia liczby naturalnej przez ułamek dziesiętny i dzielenia ułamka dziesiętnego przez liczbę naturalną nie różni się od istoty dzielenia ułamków dziesiętnych. Oznacza to, że ułamki skończone i okresowe zastępuje się ułamkami zwykłymi, a nieskończone ułamki nieokresowe są zaokrąglane.
Aby to zilustrować, rozważmy przykład dzielenia ułamka dziesiętnego przez liczbę naturalną.
Przykład.
Podziel ułamek dziesiętny 25,5 przez liczbę naturalną 45.
Rozwiązanie.
Zastępując ułamek dziesiętny 25,5 ułamkiem zwykłym 255/10=51/2, dzielenie sprowadza się do podzielenia ułamka zwykłego przez liczbę naturalną:. Wynikowy ułamek w zapisie dziesiętnym ma postać 0,5(6) .
Odpowiedź:
25,5:45=0,5(6) .
Dzielenie ułamka dziesiętnego przez liczbę naturalną za pomocą kolumny
Wygodnie jest dzielić skończone ułamki dziesiętne na liczby naturalne przez kolumnę, analogicznie do dzielenia przez kolumnę liczb naturalnych. Przedstawmy regułę dzielenia.
Do podzielić ułamek dziesiętny przez liczbę naturalną za pomocą kolumny, niezbędny:
- dodaj kilka cyfr 0 na prawo od dzielonego ułamka dziesiętnego (w trakcie dzielenia, jeśli zajdzie taka potrzeba, możesz dodać dowolną liczbę zer, ale te zera mogą nie być potrzebne);
- wykonaj dzielenie przez kolumnę ułamka dziesiętnego przez liczbę naturalną zgodnie ze wszystkimi zasadami dzielenia przez kolumnę liczb naturalnych, ale gdy dzielenie całej części ułamka dziesiętnego zostanie zakończone, wówczas w ilorazie należy umieścić przecinek i kontynuuj dzielenie.
Powiedzmy od razu, że w wyniku podzielenia skończonego ułamka dziesiętnego przez liczbę naturalną można otrzymać skończony ułamek dziesiętny lub nieskończony okresowy ułamek dziesiętny. Rzeczywiście, po zakończeniu dzielenia wszystkich miejsc po przecinku innych niż 0 dzielonego ułamka albo reszta może wynosić 0 i otrzymamy końcowy ułamek dziesiętny, albo reszty zaczną się okresowo powtarzać i otrzymamy okresowy ułamek dziesiętny.
Rozumiemy wszystkie zawiłości dzielenia ułamków dziesiętnych przez liczby naturalne w kolumnie podczas rozwiązywania przykładów.
Przykład.
Podziel ułamek dziesiętny 65,14 przez 4.
Rozwiązanie.
Podzielmy ułamek dziesiętny przez liczbę naturalną za pomocą kolumny. Dodajmy kilka zer po prawej stronie w zapisie ułamka 65,14, a otrzymamy równy ułamek dziesiętny 65,1400 (patrz równe i nierówne ułamki dziesiętne). Teraz możesz zacząć dzielić kolumną część całkowitą ułamka dziesiętnego 65,1400 przez liczbę naturalną 4: 
Na tym kończy się dzielenie części całkowitej ułamka dziesiętnego. Tutaj w ilorazie musisz umieścić przecinek dziesiętny i kontynuować dzielenie: 
Dotarliśmy do reszty wynoszącej 0, na tym etapie dzielenie przez kolumnę się kończy. W rezultacie mamy 65,14:4 = 16,285.
Odpowiedź:
65,14:4=16,285 .
Przykład.
Podziel 164,5 przez 27.
Rozwiązanie.
Podzielmy ułamek dziesiętny przez liczbę naturalną za pomocą kolumny. Po podzieleniu całej części otrzymamy następujący obraz: 
Teraz w iloraz stawiamy przecinek i kontynuujemy dzielenie kolumną: 
Teraz wyraźnie widać, że reszty 25, 7 i 16 zaczęły się powtarzać, natomiast w ilorazie powtarzają się liczby 9, 2 i 5. Zatem podzielenie liczby dziesiętnej 164,5 przez 27 daje nam okresową liczbę dziesiętną 6,0(925).
Odpowiedź:
164,5:27=6,0(925) .
Dzielenie kolumnowe ułamków dziesiętnych
Dzielenie ułamka dziesiętnego przez ułamek dziesiętny można sprowadzić do dzielenia ułamka dziesiętnego przez liczbę naturalną za pomocą kolumny. W tym celu należy pomnożyć dywidendę i dzielnik przez liczbę taką jak 10, 100, 1000 itd., tak aby dzielnik stał się liczbą naturalną, a następnie podzielić przez liczbę naturalną za pomocą kolumny. Możemy to zrobić dzięki właściwościom dzielenia i mnożenia, ponieważ a:b=(a·10):(b·10) , a:b=(a·100):(b·100) i tak dalej.
Innymi słowy, aby podzielić końcowy ułamek dziesiętny przez końcowy ułamek dziesiętny, potrzebować:
- w dzielnej i dzielniku przesuń przecinek w prawo o tyle miejsc, ile jest po przecinku w dzielniku; jeśli w dzielnej nie ma wystarczającej liczby znaków, aby przesunąć przecinek, należy dodać wymaganą liczbę zera po prawej stronie;
- Następnie podziel kolumnę dziesiętną przez liczbę naturalną.
Rozwiązując przykład, rozważ zastosowanie tej zasady dzielenia przez ułamek dziesiętny.
Przykład.
Podziel kolumną 7,287 przez 2,1.
Rozwiązanie.
Przesuńmy przecinek w tych ułamkach dziesiętnych o jedną cyfrę w prawo, co pozwoli nam przejść od dzielenia ułamka dziesiętnego 7,287 przez ułamek dziesiętny 2,1 do dzielenia ułamka dziesiętnego 72,87 przez liczbę naturalną 21. Zróbmy dzielenie według kolumn: 
Odpowiedź:
7,287:2,1=3,47 .
Przykład.
Podziel liczbę dziesiętną 16,3 przez liczbę dziesiętną 0,021.
Rozwiązanie.
Przesuń przecinek w dzielnej i dzielniku w trzy odpowiednie miejsca. Oczywiście w dzielniku nie ma wystarczającej liczby cyfr, aby przesunąć przecinek dziesiętny, dlatego dodamy wymaganą liczbę zer po prawej stronie. Teraz podzielmy ułamek 16300,0 kolumną przez liczbę naturalną 21: 
Od tego momentu reszty 4, 19, 1, 10, 16 i 13 zaczynają się powtarzać, co oznacza, że liczby 1, 9, 0, 4, 7 i 6 w ilorazu również się powtórzą. W rezultacie otrzymujemy okresowy ułamek dziesiętny 776,(190476) .
Odpowiedź:
16,3:0,021=776,(190476) .
Należy pamiętać, że ogłoszona reguła pozwala podzielić liczbę naturalną przez kolumnę na końcowy ułamek dziesiętny.
Przykład.
Podziel liczbę naturalną 3 przez ułamek dziesiętny 5.4.
Rozwiązanie.
Po przesunięciu przecinka o jedną cyfrę w prawo dochodzimy do dzielenia liczby 30,0 przez 54. Zróbmy dzielenie według kolumn: 
.
Zasadę tę można również zastosować przy dzieleniu nieskończonych ułamków dziesiętnych przez 10, 100, .... Na przykład 3,(56):1000=0,003(56) i 593,374…:100=5,93374… .
Dzielenie ułamków dziesiętnych przez 0,1, 0,01, 0,001 itd.
Ponieważ 0,1 = 1/10, 0,01 = 1/100 itd., to z zasady dzielenia przez ułamek zwykły wynika, że ułamek dziesiętny dzielimy przez 0,1, 0,01, 0,001 itd. . jest to to samo, co pomnożenie danej liczby dziesiętnej przez 10, 100, 1000 itd. odpowiednio.
Innymi słowy, aby podzielić ułamek dziesiętny przez 0,1, 0,01, ... należy przesunąć przecinek w prawo o 1, 2, 3, ... cyfry, a jeśli cyfr w ułamku dziesiętnym nie wystarczą aby przesunąć przecinek dziesiętny, musisz dodać wymaganą liczbę do odpowiednich zer.
Na przykład 5,739:0,1=57,39 i 0,21:0,00001=21 000.
Tę samą zasadę można zastosować przy dzieleniu nieskończonych ułamków dziesiętnych przez 0,1, 0,01, 0,001 itd. W takim przypadku należy zachować szczególną ostrożność przy dzieleniu ułamków okresowych, aby nie pomylić okresu ułamka powstałego w wyniku dzielenia. Przykładowo 7,5(716):0,01=757,(167), gdyż po przesunięciu przecinka w ułamku dziesiętnym 7,5716716716...dwa miejsca w prawo mamy wpis 757.167167.... Dzięki nieskończonym nieokresowym ułamkom dziesiętnym wszystko jest prostsze: 394,38283…:0,001=394382,83… .
Dzielenie ułamka zwykłego lub liczby mieszanej przez ułamek dziesiętny i odwrotnie
Dzielenie ułamka zwykłego lub liczby mieszanej przez skończony lub okresowy ułamek dziesiętny, a także dzielenie skończonego lub okresowego ułamka dziesiętnego przez ułamek zwykły lub liczbę mieszaną, sprowadza się do dzielenia ułamków zwykłych. Aby to zrobić, ułamki dziesiętne zastępuje się odpowiednimi ułamkami zwykłymi, a liczbę mieszaną przedstawia się jako ułamek niewłaściwy.
Dzieląc nieskończony nieokresowy ułamek dziesiętny przez ułamek zwykły lub liczbę mieszaną i odwrotnie, należy przystąpić do dzielenia ułamków dziesiętnych, zastępując ułamek zwykły lub liczbę mieszaną odpowiednim ułamkiem dziesiętnym.
Bibliografia.
- Matematyka: podręcznik dla 5 klasy. ogólne wykształcenie instytucje / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - wyd. 21, skreślone. - M.: Mnemosyne, 2007. - 280 s.: il. ISBN 5-346-00699-0.
- Matematyka. Klasa 6: edukacyjna. dla edukacji ogólnej instytucje / [N. Tak, Vilenkin i inni]. - wyd. 22, wyd. - M.: Mnemosyne, 2008. - 288 s.: il. ISBN 978-5-346-00897-2.
- Algebra: podręcznik dla 8 klasy. ogólne wykształcenie instytucje / [Yu. N. Makaryczew, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edytowany przez SA Telyakovsky. - wyd. 16. - M.: Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
- Gusiew V. A., Mordkovich A. G. Matematyka (podręcznik dla rozpoczynających naukę w technikach): Proc. zasiłek.- M.; Wyższy szkoła, 1984.-351 s., il.
Wiele dzieci w wieku szkolnym zapomina, jak dzielić przez długi czas, zanim pójdą do szkoły średniej. Komputery, kalkulatory, telefony komórkowe i inne urządzenia stały się tak integralną częścią naszego życia, że podstawowe operacje matematyczne czasami wprawiają nas w osłupienie. A jak kilka dekad temu ludzie radzili sobie bez tych wszystkich korzyści? Najpierw musisz pamiętać główne pojęcia matematyczne potrzebne do dzielenia. Zatem dywidenda to liczba, która zostanie podzielona. Dzielnik – liczba, przez którą należy dzielić. Wynik nazywany jest ilorazem. Aby podzielić na linię, użyj symbolu podobnego do dwukropka - „:”, a przy podziale na kolumnę użyj ikony „∟”, zwanej również narożnikiem.
Warto również przypomnieć, że każde dzielenie można sprawdzić przez mnożenie. Aby sprawdzić wynik dzielenia, wystarczy pomnożyć go przez dzielnik; wynikiem powinna być liczba odpowiadająca dzielnej (a: b=c; zatem c*b=a). Teraz o tym, czym jest ułamek dziesiętny. Ułamek dziesiętny otrzymuje się dzieląc jednostkę przez 0,0, 1000 i tak dalej. Zapisywanie tych liczb i operacje matematyczne na nich są dokładnie takie same, jak w przypadku liczb całkowitych. Dzieląc ułamki dziesiętne, nie trzeba pamiętać, gdzie znajduje się mianownik. Wszystko staje się jasne, gdy zapiszesz numer. Najpierw zapisuje się liczbę całkowitą, a po przecinku zapisuje się jej części dziesiąte, setne, tysięczne. Pierwsza cyfra po przecinku odpowiada dziesiątkom, druga setkom, trzecia tysiącom itd.
Każdy uczeń powinien wiedzieć, jak dzielić ułamki dziesiętne przez ułamki dziesiętne. Jeśli zarówno dywidenda, jak i dzielnik zostaną pomnożone przez tę samą liczbę, wówczas odpowiedź, tj. Iloraz, nie ulegnie zmianie. Jeśli ułamek dziesiętny zostanie pomnożony przez 0,0, 1000 itd., to przecinek po liczbie całkowitej zmieni swoje położenie - przesunie się w prawo o tę samą liczbę cyfr, ile jest zer w liczbie, przez którą pomnożono. Na przykład podczas mnożenia ułamka dziesiętnego przez 10 przecinek dziesiętny przesunie się o jedną liczbę w prawo. 2,9:6,7 – mnożymy zarówno dzielnik, jak i dywidendę przez 100, otrzymamy 6,9:3687. Najlepiej pomnożyć tak, aby po pomnożeniu przez nią przynajmniej jedna liczba (dzielnik lub dywidenda) nie miała już cyfr po przecinku , tj. uczyń co najmniej jedną liczbę liczbą całkowitą. Jeszcze kilka przykładów przesuwania przecinków po liczbie całkowitej: 9,2: 1,5 = 2492: 2,5; 5,4:4,8 = 5344:74598.
Uwaga, ułamek dziesiętny nie zmieni swojej wartości, jeśli do prawej strony dodamy zera, np. 3,8 = 3,0. Również wartość ułamka nie ulegnie zmianie, jeśli z prawej strony zostaną usunięte zera na samym końcu liczby: 3,0 = 3,3. Nie można jednak usunąć zer ze środka liczby - 3.3. Jak podzielić ułamek dziesiętny przez liczbę naturalną w kolumnie? Aby podzielić ułamek dziesiętny przez liczbę naturalną w kolumnie, należy dokonać odpowiedniego zapisu z narożnikiem, podzielić. W ilorazie należy postawić przecinek, gdy kończy się dzielenie liczby całkowitej. Przykładowo 5,4|2 14 7,2 18 18 0 4 4 0Jeżeli pierwsza cyfra liczby w dzielnej jest mniejsza od dzielnika, to stosuje się kolejne cyfry, aż będzie można wykonać pierwszą akcję.
W tym przypadku pierwszą cyfrą dywidendy jest 1, nie można jej podzielić przez 2, dlatego do dzielenia używa się jednocześnie dwóch cyfr 1 i 5: 15 dzieli się przez 2 z resztą, okazuje się, że jest to iloraz 7, a reszta pozostaje 1. Następnie wykorzystujemy kolejną cyfrę dzielnej - 8. Obniżamy ją do 1 i dzielimy 18 przez 2. W ilorazu zapisujemy liczbę 9. W pozostałej części nic nie zostaje, więc piszemy 0. Pozostałą liczbę 4 dywidendy obniżamy i dzielimy przez dzielnik, czyli przez 2. W iloraz zapisujemy 2, a reszta znowu wynosi 0. Wynikiem tego dzielenia jest liczba 7,2. To się nazywa prywatne. Rozwiązanie problemu dzielenia ułamka dziesiętnego przez ułamek dziesiętny jest dość łatwe, jeśli znasz kilka sztuczek. Dzielenie ułamków dziesiętnych w myślach jest czasami dość trudne, dlatego stosuje się długie dzielenie, aby ułatwić ten proces.
Przy tym dzieleniu obowiązują te same zasady, co przy dzieleniu ułamka dziesiętnego przez liczbę całkowitą lub przy dzieleniu na ciąg znaków. Po lewej stronie linii zapisują dywidendę, następnie umieszczają symbol „roga”, a następnie wpisują dzielnik i rozpoczynają dzielenie. Aby ułatwić dzielenie i przenieść przecinek po liczbie całkowitej w dogodne miejsce, możesz pomnożyć przez dziesiątki, setki lub tysiące. Na przykład 9,2: 1,5 = 24920: 125. Uwaga, oba ułamki mnoży się przez 0,0, 1000. Jeżeli dywidendę pomnożono przez 10, to dzielnik również pomnożono przez 10. W tym przykładzie zarówno dywidendę, jak i dzielnik pomnożono przez 100. Następnie obliczenia wykonuje się w taki sam sposób, jak pokazano w przykładzie dzielenia ułamek dziesiętny przez liczbę naturalną. Aby podzielić przez 0,1; 0,1; 0,1 itd. należy pomnożyć zarówno dzielnik, jak i dywidendę przez 0,0, 1000.
Dość często, dzieląc przez iloraz, tj. w odpowiedzi, uzyskuje się nieskończone ułamki. W takim przypadku konieczne jest zaokrąglenie liczby do części dziesiątych, setnych lub tysięcznych. W tym przypadku obowiązuje zasada: jeśli po liczbie, do której należy zaokrąglić odpowiedź, jest mniejsza lub równa 5, wówczas odpowiedź jest zaokrąglana w dół, a jeśli jest większa niż 5, jest zaokrąglana w górę. Na przykład chcesz zaokrąglić wynik 5,5 do części tysięcznych. Oznacza to, że odpowiedź po przecinku powinna kończyć się cyfrą 6. Po 6 jest 9, co oznacza, że zaokrąglamy odpowiedź w górę i otrzymujemy 5,7. Ale gdyby odpowiedź 5,5 trzeba było zaokrąglić nie do tysięcznych, ale do dziesiątych, to odpowiedź wyglądałaby tak - 5,2. W tym przypadku 2 nie zostało zaokrąglone w górę, ponieważ po nim następuje 3, a jest to mniej niż 5.
Każda część.
Rozwiązanie. Aby rozwiązać problem, wyraźmy długość taśmy w decymetrach: 19,2 m = 192 dm. Ale 192: 8 = 24. Oznacza to, że długość każdej części wynosi 24 dm,
czyli 2,4 m. Jeśli pomnożymy 2,4 przez 8, otrzymamy 19,2. Zatem 2,4 jest ilorazem 19,2 podzielonym przez 8.
Piszą: 19,2: 8 = 2,4.
Tę samą odpowiedź można uzyskać bez przeliczania liczników na decymetry. Aby to zrobić, musisz podzielić 19,2 przez 8, nie zwracając uwagi na przecinek, i wstawić przecinek w iloraz, gdy zakończy się dzielenie całej części:
Dzielenie ułamka dziesiętnego przez liczbę naturalną oznacza znalezienie ułamka, który pomnożony przez tę liczbę naturalną daje dywidendę.
Aby podzielić ułamek dziesiętny przez liczbę naturalną, należy:
1) podziel ułamek przez tę liczbę, ignorując przecinek;
2) w ilorazu, gdy kończy się dzielenie całej części, wstawić przecinek;
Jeśli część całkowita jest mniejsza niż dzielnik, wówczas iloraz zaczyna się od zerowych liczb całkowitych:
Podziel 96,1 przez 10. Jeśli pomnożysz iloraz przez 10, powinieneś ponownie otrzymać 96,1.
Innymi słowy, dzielenie służy do zamiany ułamka zwykłego na dziesiętny.
Przykład. Zamień ułamek zwykły na dziesiętny.
Rozwiązanie. Ułamek jest ilorazem 3 podzielonym przez 4. Dzielenie 3 przez 4 daje ułamek dziesiętny 0,75. Zatem = 0,75.
Co to znaczy dzielić ułamek dziesiętny przez liczbę naturalną?
Jak podzielić ułamek dziesiętny przez liczbę naturalną?
Jak podzielić ułamek dziesiętny przez 10, 100, 1000?
Jak zamienić ułamek zwykły na dziesiętny?
1340. Dokonaj podziału:
a) 20,7: 9;
b) 243,2: 8;
c) 88,298:7;
d) 772,8:12;
e) 93,15:23;
e) 0,644: 92;
g) 1: 80;
h) 0,909:45;
i) 3: 32;
j) 0,01242: 69;
l) 1,016: 8;
m) 7,368:24.
1341. Na samolot na wyprawę polarną załadowano 3 ciągniki o wadze 1,2 tony każdy i 7 skuterów śnieżnych. Masa wszystkich skuterów śnieżnych jest o 2 tony większa niż masa traktorów. Jaka jest masa jednego skutera śnieżnego?
a) 4x - x = 8,7; c) a + a + 8,154 = 32;
b) Zu + bу = 9,6; d) 7 tys. - 4 tys. - 55,2 = 63,12.
1349. W dwóch koszach jest 16,8 kg pomidorów. W jednym koszu jest dwa razy więcej pomidorów niż w drugim. Ile kilogramów pomidorów znajduje się w każdym koszyku?
1350. Powierzchnia pierwszego pola jest 5 razy większa niż powierzchnia drugiego. Jaka jest powierzchnia każdego pola, jeśli kwadrat druga jest o 23,2 ha mniejsza od powierzchni pierwszej?
1351. Do przygotowania kompotu przygotowano mieszankę z 8 części (wagowo) suszonych jabłek, 4 części moreli i 3 części rodzynek. Ile kilogramów każdego suszu potrzeba było na 2,7 kg takiej mieszanki?
1352. W dwóch workach znajduje się 1,28 kwintala mąki. Pierwszy worek zawiera o 0,12 kwintala więcej mąki niż drugi. Ile kwintali mąki jest w każdym worku?
1353. W dwóch koszach jest 18,6 kg jabłek. Pierwszy koszyk jabłek zawiera o 2,4 kg mniej niż drugi. Ile kilogramów jabłek jest w każdym koszyku?
1354. Wyraź w postaci ułamka dziesiętnego:
1355. Aby zebrać 100 g miodu, pszczoła dostarcza do ula 16 tys. ładunków nektaru. Czym jest jeden ładunek nektaru?
1356. Butelka zawiera 30 g leku. Znajdź masę jednej kropli leku, jeśli w butelce znajduje się 1500 kropli.
1357. Przedstaw ułamek zwykły jako ułamek dziesiętny i wykonaj następujące kroki:
1358. Rozwiąż równanie:
a) (x - 5,46) -2 = 9;
b) (y + 0,5): 2 = 1,57.
1359. Znajdź znaczenie wyrażenia:
a) 91,8: (10,56 - 1,56) + 0,704; e) 15,3 -4:9 + 3,2;
b) (61,5 - 5,16): 30 + 5,05; e) (4,3 + 2,4: 8) 3;
c) 66,24 - 16,24: (3,7 + 4,3); g) 280,8: 12 - 0,3 24;
d) 28,6 + 11,4: (6,595 + 3,405); h) (17,6 · 13 - 41,6): 12.
1360. Oblicz ustnie:
a) 2,5 - 1,6; b) 1,8 + 2,5; c) 3,4 - 0,2; d) 5 + 0,35;
3,2 - 1,4; 2,7 + 1,6; 2,6 - 0,05; 3,7 + 0,24;
0,47 - 0,27; 0,63 + 0,17; 4,52 - 1,2; 0,46 + 1,8;
0,64-0,15; 0,38 + 0,29; 4-0,8; 0,57 + 3;
0,71 - 0,28; 0,55 + 0,45; 1 - 0,45; 1,64 + 0,36.
a) 0,3 2; d) 2,3 3; g) 3,7 10; i) 0,18 5;
b) 0,8 3; e) 0,21 4; h) 0,09 6; j) 0,87 0.
c) 1,2 2; e) 1,6 5;
1362. Zgadnij, jakie są pierwiastki równania:
a) 2,9x = 2,9; c) 3,7x = 37; e) a3 = a;
b) 5,25x = 0; d) x 2 = x e) m 2 = m 3.
1363. Jak zmieni się wartość wyrażenia 2.5a, jeżeli a: zwiększymy o 1? zwiększyć o 2? wzrosnąć 2 razy?
1364. Powiedz nam, jak oznaczyć liczbę na belce współrzędnych: 0,25; 0 5; 0,75. Zastanów się, które z podanych liczb są równe. Jaki ułamek o mianowniku 4 równa się 0,5? Zginać: 
1365. Pomyśl o zasadzie, według której składa się ciąg liczb, i zapisz jeszcze dwie liczby z tego ciągu:
a) 1,2; 1,8; 2,4; 3; ... c) 0,9; 1,8; 3,6; 7,2; ...
b) 9,6; 8,9; 8,2; 7,5; ... d) 1,2; 0,7; 2,2; 1,4; 3,2; 2.1; ...
1366. Wykonaj następujące kroki:
a) (37,8 - 19,1) 4; c) (64,37 + 33,21 - 21,56) 14;
b) (14,23 + 13,97) 31; d) (33,56 - 18,29) (13,2 + 24,9 - 38,1).
a) 3,705; 62,8; 0,5 razy 10;
b) 2,3578; 0,0068; 0,3 na 100 razy.
1368. Zaokrąglij liczbę 82 719,364:
a) do jednostek; c) do dziesiątych; d) do tysięcy.
b) do setek; d) do setnych;
1369. Wykonaj czynność:
1370. Porównaj:
1371. Kola, Petya, Żenia i Senya zważyli się na wadze. Wyniki były następujące: 37,7 kg; 42,5 kg; 39,2 kg; 40,8 kg. Znajdź masę każdego chłopca, jeśli wiadomo, że Kola jest cięższa od Senyi i lżejsza od Petyi, a Żenia jest lżejsza od Senyi.
1372. Uprość wyrażenie i znajdź jego znaczenie:
a) 23,9 - 18,55 - mt jeśli t = 1,64;
b) 16,4 + k + 3,8, jeśli k = 2,7.
1373. Rozwiąż równanie:
a) 16,1 - (x - 3,8) = 11,3;
b) 25,34 - (2,7 + y) = 15,34.
1374. Znajdź znaczenie wyrażenia:
1) (1070 - 104 040: 2312) 74 + 6489;
2) (38 529 + 205 87) : 427 - 119.
1375. Dokonaj podziału:
a) 53,5: 5; e) 0,7:25; i) 9,607: 10;
b) 1,75:7; e) 7,9: 316; j) 14,706: 1000;
c) 0,48:6; g) 543,4: 143; l) 0,0142: 100;
d) 13,2: 24; h) 40,005: 127; m) 0,75: 10 000.
1376. Samochód jechał autostradą przez 3 godziny z prędkością 65,8 km/h, a następnie przez 5 godzin jechał drogą gruntową. Z jaką prędkością szła polną drogą, jeśli cała jej droga miała 324,9 km?
1377. W magazynie znajdowało się 180,4 ton węgla. Węgiel ten dostarczano do ciepłowni szkół. Ile ton węgla zostało w magazynie?
1378. Pola zostały zaorane. Znajdź powierzchnię tego pola, jeśli zaorano 32,5 ha.
1379. Rozwiąż równanie:
a) 15x = 0,15; f) 8p - 2p - 14,21 = 75,19;
b) 3,08: y = 4; g) 295,1: (n - 3) = 13;
c) Dla + 8a = 1,87; h) 34 (m + 1,2) = 61,2;
d) 7z - 3z = 5,12; i) 15 (k - 0,2) = 21.
e) 2t + 5t + 3,18 = 25,3;
1380. Znajdź znaczenie wyrażenia:
a) 0,24: 4 + 15,3: 5 + 12,4: 8 + 0,15: 30;
b) (1,24 + 3,56): 16;
c) 2,28 + 3,72: 12;
d) 3,6 4-2,4: (11,7 - 3,7).
1381. Z trzech łąk zebrano 19,7 ton siana. Z pierwszej i drugiej łąki zebraliśmy równą ilość siana, z trzeciej o 1,1 tony więcej niż z każdej z dwóch pierwszych. Ile siana zebrano z każdej łąki?
1382. W ciągu 3 dni sklep sprzedał 1240,8 kg cukru. Pierwszego dnia sprzedano 543 kg, drugiego – 2 razy więcej niż trzeciego. Ile kilogramów cukru sprzedano trzeciego dnia?
1383. Pierwszy odcinek trasy samochód pokonał w 3 godziny, drugi w 2 h. Łączna długość obu odcinków wynosi 267 km. Z jaką prędkością jechał samochód na każdym odcinku, jeżeli na drugim odcinku prędkość była o 8,5 km/h większa niż na pierwszym?
1384. Konwersja na ułamki dziesiętne;
1385. Zbuduj figurę równą figurze pokazanej na rycinie 151.
1386. Rowerzysta opuścił miasto z prędkością 13,4 km/h. Po 2 godzinach za nim podążał kolejny rowerzysta, który jechał z prędkością 17,4 km/h. Poprzez
Po ilu godzinach od wyjazdu drugi rowerzysta dogoni pierwszego?
1387. Łódź, płynąc pod prąd, w ciągu 6 godzin przepłynęła 177,6 km. Znajdź własną prędkość łodzi, jeśli aktualna prędkość wynosi 2,8 km/h.
1388. Kran dostarczający 30 litrów wody na minutę napełnił wannę w ciągu 5 minut. Następnie zakręcono kran i otwarto otwór spustowy, przez który w ciągu 6 minut wylała się cała woda. Ile litrów wody wlano w ciągu 1 minuty?
1389. Rozwiąż równanie:
a) 26 (x + 427) = 15756; c) 22374: (k - 125) = 1243;
b) 101 (351 + y) = 65549; d) 38 007: (4223 - t) = 9.
N.Ya. VILENKIN, V. I. ZHOKHOV, A. S. CHESNOKOV, S. I. SHVARTSBURD, Matematyka klasa 5, Podręcznik dla instytucji kształcenia ogólnego
Pobieranie filmów z matematyki, zadania domowe, pomoc dla nauczycieli i uczniów
W tym artykule przyjrzymy się tak ważnej operacji na ułamkach dziesiętnych, jak dzielenie. Najpierw sformułowamy ogólne zasady, następnie przeanalizujemy, jak poprawnie dzielić ułamki dziesiętne w kolumnie zarówno przez inne ułamki zwykłe, jak i przez liczby naturalne. Następnie przeanalizujemy podział ułamków zwykłych na dziesiętne i odwrotnie, a na koniec przyjrzymy się, jak poprawnie dzielić ułamki kończące się na 0, 1, 0, 01, 100, 10 itd.
Tutaj będziemy brać tylko przypadki z ułamkami dodatnimi. Jeśli przed ułamkiem znajduje się minus, to aby z nim pracować, musisz przestudiować materiał na temat dzielenia liczb wymiernych i rzeczywistych.
Yandex.RTB R-A-339285-1
Wszystkie ułamki dziesiętne, zarówno skończone, jak i okresowe, są po prostu specjalną formą zapisywania ułamków zwykłych. Dlatego podlegają tym samym zasadom, co odpowiadające im ułamki zwykłe. Sprowadzamy zatem cały proces dzielenia ułamków dziesiętnych do zastąpienia ich zwykłymi, a następnie obliczenia znanymi nam metodami. Weźmy konkretny przykład.
Przykład 1
Podziel 1,2 przez 0,48.
Rozwiązanie
Zapiszmy ułamki dziesiętne jako ułamki zwykłe. Dostaniemy:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Zatem musimy podzielić 6 5 przez 12 25. Liczymy:
1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2
Z powstałego ułamka niewłaściwego możesz wybrać całą część i uzyskać liczbę mieszaną 2 1 2 lub możesz przedstawić ją jako ułamek dziesiętny, aby odpowiadał pierwotnym liczbom: 5 2 = 2, 5. O tym, jak to zrobić, pisaliśmy już wcześniej.
Odpowiedź: 1 , 2: 0 , 48 = 2 , 5 .
Przykład 2
Oblicz, ile będzie wynosić 0 , (504) 0 , 56.
Rozwiązanie
Najpierw musimy zamienić okresowy ułamek dziesiętny na ułamek zwykły.
0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
Następnie przekonwertujemy również końcowy ułamek dziesiętny na inną postać: 0, 56 = 56,100. Teraz mamy dwie liczby, dzięki którym łatwo będzie nam przeprowadzić niezbędne obliczenia:
0 , (504): 1, 11 = 56 111: 56 100 = 56 111 100 56 = 100 111
Otrzymaliśmy wynik, który możemy również zamienić na postać dziesiętną. Aby to zrobić, podziel licznik przez mianownik, stosując metodę kolumnową:
Odpowiedź: 0 , (504) : 0 , 56 = 0 , (900) .
Jeśli w przykładzie dzielenia napotkaliśmy nieokresowe ułamki dziesiętne, to zachowamy się trochę inaczej. Nie możemy ich sprowadzić do zwykłych ułamków zwykłych, dlatego dzieląc musimy je najpierw zaokrąglić do określonej cyfry. Czynność tę należy wykonać zarówno z dywidendą, jak i dzielnikiem: dla zachowania dokładności zaokrąglimy również istniejący ułamek skończony lub okresowy.
Przykład 3
Znajdź, ile to jest 0,779... / 1,5602.
Rozwiązanie
Najpierw zaokrąglamy oba ułamki do najbliższej setnej. Oto jak przechodzimy od nieskończonych ułamków nieokresowych do skończonych ułamków dziesiętnych:
0 , 779 … ≈ 0 , 78
1 , 5602 ≈ 1 , 56
Możemy kontynuować obliczenia i uzyskać przybliżony wynik: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78 100: 156 100 = 78 100 100 156 = 78 156 = 1 2 = 0, 5.
Dokładność wyniku będzie zależeć od stopnia zaokrąglenia.
Odpowiedź: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Jak podzielić liczbę naturalną przez ułamek dziesiętny i odwrotnie
Podejście do dzielenia w tym przypadku jest prawie takie samo: ułamki skończone i okresowe zastępujemy ułamkami zwyczajnymi, a nieskończone ułamki nieokresowe zaokrąglamy. Zacznijmy od przykładu dzielenia liczby naturalnej i ułamka dziesiętnego.
Przykład 4
Podziel 2,5 przez 45.
Rozwiązanie
Sprowadźmy 2, 5 do postaci ułamka zwykłego: 255 10 = 51 2. Następnie wystarczy podzielić to przez liczbę naturalną. Wiemy już jak to zrobić:
25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30
Jeśli przekonwertujemy wynik na zapis dziesiętny, otrzymamy 0,5 (6).
Odpowiedź: 25 , 5: 45 = 0 , 5 (6) .
Metoda długiego dzielenia sprawdza się nie tylko w przypadku liczb naturalnych. Przez analogię możemy go używać do ułamków zwykłych. Poniżej wskazujemy sekwencję działań, które należy w tym celu wykonać.
Definicja 1
Aby podzielić kolumnę ułamków dziesiętnych przez liczby naturalne, potrzebujesz:
1. Do ułamka dziesiętnego po prawej stronie dodaj kilka zer (do dzielenia możemy dodać dowolną ich liczbę).
2. Podziel ułamek dziesiętny przez liczbę naturalną, korzystając z algorytmu. Kiedy dzielenie całej części ułamka dobiegnie końca, w powstałym ilorazie stawiamy przecinek i liczymy dalej.
Wynikiem takiego podziału może być skończona lub nieskończona okresowa część dziesiętna. Zależy to od reszty: jeśli wynosi zero, wynik będzie skończony, a jeśli reszty zaczną się powtarzać, wówczas odpowiedzią będzie ułamek okresowy.
Weźmy na przykład kilka problemów i spróbujmy wykonać te kroki z konkretnymi liczbami.
Przykład 5
Oblicz, ile będzie 65, 14 4.
Rozwiązanie
Stosujemy metodę kolumnową. Aby to zrobić, dodaj dwa zera do ułamka i uzyskaj ułamek dziesiętny 65, 1400, który będzie równy pierwotnemu. Teraz piszemy kolumnę do dzielenia przez 4:
Wynikowa liczba będzie wynikiem, którego potrzebujemy z podzielenia części całkowitej. Stawiamy przecinek, oddzielając go i kontynuujemy:
Osiągnęliśmy zero, dlatego proces dzielenia został zakończony.
Odpowiedź: 65 , 14: 4 = 16 , 285 .
Przykład 6
Podziel 164,5 przez 27.
Rozwiązanie
Najpierw dzielimy część ułamkową i otrzymujemy:
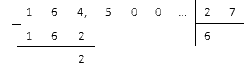
Otrzymaną liczbę oddziel przecinkiem i kontynuuj dzielenie:
Widzimy, że reszty zaczęły się okresowo powtarzać, a w ilorazie liczby dziewięć, dwa i pięć zaczęły się zmieniać. Zatrzymamy się tutaj i napiszemy odpowiedź w postaci ułamka okresowego 6, 0 (925).
Odpowiedź: 164 , 5: 27 = 6 , 0 (925) .
Podział ten można sprowadzić do opisanego już powyżej procesu znajdowania ilorazu ułamka dziesiętnego i liczby naturalnej. Aby to zrobić, musimy pomnożyć dywidendę i dzielnik przez 10, 100 itd., aby dzielnik zamienił się w liczbę naturalną. Następnie wykonujemy sekwencję czynności opisaną powyżej. Takie podejście jest możliwe dzięki właściwościom dzielenia i mnożenia. Zapisaliśmy je w ten sposób:
a: b = (a · 10): (b · 10) , a: b = (a · 100): (b · 100) i tak dalej.
Sformułujmy regułę:
Definicja 2
Aby podzielić ostatni ułamek dziesiętny przez inny:
1. Przesuń przecinek w dzielnej i dzielniku w prawo o liczbę cyfr niezbędną do zamiany dzielnika na liczbę naturalną. Jeśli w dywidendzie nie ma wystarczającej liczby znaków, dodajemy do niej zera po prawej stronie.
2. Następnie podziel ułamek przez kolumnę przez wynikową liczbę naturalną.
Spójrzmy na konkretny problem.
Przykład 7
Podziel 7,287 przez 2,1.
Rozwiązanie: Aby dzielnik był liczbą naturalną, musimy przesunąć przecinek o jedno miejsce w prawo. Przeszliśmy więc do dzielenia ułamka dziesiętnego 72, 87 przez 21. Zapiszmy wynikowe liczby w kolumnie i obliczmy
Odpowiedź: 7 , 287: 2 , 1 = 3 , 47
Przykład 8
Oblicz 16.30.021.
Rozwiązanie
Będziemy musieli przesunąć przecinek o trzy miejsca. W dzielniku nie ma wystarczającej liczby cyfr, co oznacza, że należy użyć dodatkowych zer. Uważamy, że wynikiem będzie:
Widzimy okresowe powtarzanie reszt 4, 19, 1, 10, 16, 13. W ilorazie powtarzają się 1, 9, 0, 4, 7 i 5. Wtedy naszym wynikiem będzie okresowy ułamek dziesiętny 776, (190476).
Odpowiedź: 16 , 3: 0 , 021 = 776 , (190476)
Opisana przez nas metoda pozwala zrobić coś odwrotnego, to znaczy podzielić liczbę naturalną przez końcowy ułamek dziesiętny. Zobaczmy jak to się robi.
Przykład 9
Oblicz, ile to jest 3 5, 4.
Rozwiązanie
Oczywiście będziemy musieli przesunąć przecinek w jedno właściwe miejsce. Następnie możemy przystąpić do dzielenia 30, 0 przez 54. Zapiszmy dane w kolumnie i obliczmy wynik:
Powtarzanie reszty daje nam ostateczną liczbę 0, (5), która jest okresowym ułamkiem dziesiętnym.
Odpowiedź: 3: 5 , 4 = 0 , (5) .
Jak dzielić ułamki dziesiętne przez 1000, 100, 10 itd.
Zgodnie z już przestudiowanymi zasadami dzielenia ułamków zwykłych, dzielenie ułamka przez dziesiątki, setki, tysiące jest podobne do pomnożenia go przez 1/1000, 1/100, 1/10 itd. Okazuje się, że aby wykonać dzielenie, w w tym przypadku wystarczy po prostu przesunąć przecinek dziesiętny do wymaganych liczb Jeśli w liczbie do przeniesienia nie ma wystarczającej liczby wartości, musisz dodać wymaganą liczbę zer.
Przykład 10
Zatem 56, 21: 10 = 5, 621 i 0, 32: 100 000 = 0, 0000032.
W przypadku nieskończonych ułamków dziesiętnych postępujemy tak samo.
Przykład 11
Na przykład 3, (56): 1000 = 0, 003 (56) i 593, 374...: 100 = 5, 93374....
Jak dzielić ułamki dziesiętne przez 0,001, 0,01, 0,1 itd.
Korzystając z tej samej zasady, możemy również dzielić ułamki na wskazane wartości. Ta czynność będzie podobna do mnożenia odpowiednio przez 1000, 100, 10. Aby to zrobić, przesuwamy przecinek na jedną, dwie lub trzy cyfry, w zależności od warunków zadania i dodajemy zera, jeśli w liczbie nie ma wystarczającej liczby cyfr.
Przykład 12
Na przykład 5,739: 0,1 = 57,39 i 0,21: 0,00001 = 21 000.
Zasada ta dotyczy również nieskończonych ułamków dziesiętnych. Radzimy jedynie uważać na okres ułamka, który pojawia się w odpowiedzi.
Czyli 7, 5 (716): 0, 01 = 757, (167), bo po przesunięciu przecinka w ułamku dziesiętnym 7, 5716716716... dwa miejsca w prawo otrzymaliśmy 757, 167167....
Jeśli w przykładzie mamy ułamki nieokresowe, to wszystko jest prostsze: 394, 38283...: 0, 001 = 394382, 83....
Jak podzielić liczbę mieszaną lub ułamek przez ułamek dziesiętny i odwrotnie
Sprowadzamy to działanie również do operacji na ułamkach zwykłych. Aby to zrobić, musisz zastąpić liczby dziesiętne odpowiednimi ułamkami zwykłymi i zapisać liczbę mieszaną jako ułamek niewłaściwy.
Jeśli dzielimy ułamek nieokresowy przez liczbę zwykłą lub mieszaną, musimy zrobić odwrotnie, zastępując ułamek zwykły lub liczbę mieszaną odpowiednim ułamkiem dziesiętnym.
Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter
I. Aby podzielić ułamek dziesiętny przez liczbę naturalną, należy podzielić ułamek przez tę liczbę, tak jak dzielą się liczby naturalne, a po zakończeniu dzielenia całej części wstawić przecinek w iloraz.
Przykłady.
Wykonaj dzielenie: 1) 96,25: 5; 2) 4,78: 4; 3) 183,06: 45.
Rozwiązanie.
Przykład 1) 96,25: 5.
Dzielimy za pomocą „rogu” w taki sam sposób, jak dzieli się liczby naturalne. Po tym jak usuniemy numer 2 (liczba dziesiątych to pierwsza cyfra po przecinku w dywidendzie 96, 2 5), w ilorazie stawiamy przecinek i kontynuujemy dzielenie.
Odpowiedź: 19,25.
Przykład 2) 4,78: 4.
Dzielimy się tak, jak dzielą się liczby naturalne. W ilorazie wstawimy przecinek, gdy tylko go usuniemy 7
— pierwsza cyfra po przecinku w dywidendzie 4, 7
8. Kontynuujemy podział dalej. Odejmując 38-36 otrzymamy 2, ale dzielenie nie jest zakończone. Jak postępować? Wiemy, że na końcu ułamka dziesiętnego można dodać zera – nie zmieni to wartości ułamka. Przypisujemy zero i dzielimy 20 przez 4. Otrzymujemy 5 - dzielenie się kończy.
Odpowiedź: 1,195.
Przykład 3) 183,06: 45.
Podziel jako 18306 przez 45. W ilorazie stawiamy przecinek, gdy tylko usuniemy liczbę 0
— pierwsza cyfra po przecinku w dywidendzie 183, 0
6. Podobnie jak w przykładzie 2) musieliśmy przypisać zero liczbie 36 – różnicy pomiędzy liczbami 306 i 270.
Odpowiedź: 4,068.
Wniosek: podczas dzielenia ułamka dziesiętnego przez liczbę naturalną w prywatny, stawiamy przecinek zaraz po odjęciu liczby dziesiątej części dywidendy. Uwaga: wszystkie wyróżnione cyfry na czerwono w tych trzech przykładach należą do tej kategorii dziesiątych dywidendy.
II. Aby podzielić ułamek dziesiętny przez 10, 100, 1000 itd., należy przesunąć przecinek w lewo o 1, 2, 3 itd. cyfry.
Przykłady.
Wykonaj dzielenie: 1) 41,56: 10; 2) 123,45: 100; 3) 0,47: 100; 4) 8,5: 1000; 5) 631,2: 10000.
Rozwiązanie.
Przesunięcie przecinka w lewo zależy od tego, ile zer po jedynce znajduje się w dzielniku. Zatem dzieląc ułamek dziesiętny przez 10
przeniesiemy w formie dywidendy przecinek w lewo o jedną cyfrę; przy dzieleniu przez 100
- przesuń przecinek zostawił dwie cyfry; przy dzieleniu przez 1000
zamień na ten ułamek dziesiętny przecinek trzy cyfry w lewo.