Решение неравенств. Неравенства бывают разных видов и требуют разного подхода к их решению. Если вы не желаете тратить время и силы на решение неравенств или решили неравенство самостоятельно и хотите проверить, верный ли ответ вы получили, то предлагаем вам решать неравенства онлайн и воспользоваться для этого нашим сервисом Math24.su. Он решает как линейные, так и квадратные неравенства, в том числе иррациональные и дробные неравенства. Обязательно укажите обе части неравенства в соответствующих полях и выберете знак неравенства между ними, затем нажмите кнопку «Решение». Чтобы продемонстрировать как в сервисе реализовано решение неравенств, можно просмотреть различные виды примеров и их решений (выбираются справа от кнопки «Решение»). Сервис выдает как интервалы решения, так и целочисленные значения. Пользователи, которые попадают на Math24.su впервые, восхищаются высокой скоростью работы сервиса, ведь решить неравенства онлайн можно за считанные секунды, а пользоваться сервисом можно абсолютно бесплатно неограниченное количество раз. Работа сервиса автоматизирована, вычисление в нем делает программа, а не человек. Вам не нужно устанавливать себе на компьютер какое-либо программное обеспечение, регистрироваться, вводить личные данные или e-mail. Также исключены опечатки и ошибки в расчетах, полученному результату можно доверять на 100%. Преимущества решения неравенств онлайн. Благодаря высокой скорости и удобству использования сервис Math24.su стал надежным помощником многих школьников и студентов. Неравенства часто встречаются в школьных программах и курсе института по высшей математике и те, кто использует наш онлайн сервис, получают большие преимущества перед остальными. Math24.su доступен круглосуточно, не требует регистрации, платы за использование и вдобавок мультиязычен. Не стоит пренебрегать онлайн сервисом и тем, кто ищет решение неравенств самостоятельно. Ведь Math24.su – это отличная возможность проверить правильность своих вычислений, найти, где совершена ошибка, просмотреть, как решаются различные виды неравенств. Еще одна причина, по которой будет более рационально решать неравенства онлайн, это когда решение неравенств не является основной задачей, а только ее частью. В этом случае просто нет смысла тратить много времени и сил на вычисление, а лучше доверить его онлайн сервису, в то время как самому сосредоточиться на решении основной задачи. Как видно, онлайн сервис для решения неравенств будет полезен как тем, кто самостоятельно решает данный вид математических задач, так и тем, кто не хочет тратить время и усилия на длительные расчеты, а нуждается в быстром получении ответа. Поэтому, когда вы сталкиваетесь с неравенствами, то не забывайте использовать наш сервис, чтобы решать любые неравенства онлайн: линейные, квадратные, иррациональные, тригонометрические, логарифмические. Что такое неравенства и как они обозначаются. Неравенство выступает обратной стороной равенства и как понятие связано со сравнением двух объектов. В зависимости от характеристик сравниваемых объектов, мы говорим выше, ниже, короче, длиннее, толще, тоньше и т.д. В математике смысл неравенств не теряется, но здесь речь идет уже про неравенства математических объектов: числа, выражения, значения величин, фигур и т.д. Принято использовать несколько знаков неравенств: , ≤, ≥. Математические выражения с такими знаками и называют неравенствами. Знак > (больше) ставится между большим и меньшим объектами, Знак обозначают строгие неравенства. Нестрогие неравенства описывают ситуацию, когда одно выражение «не больше» («не меньше») другого. «Не больше» означает, что меньше или столько же, а «не меньше» значит, что больше или столько же.
В статье рассмотрим решение неравенств . Расскажем доступно о том, как строиться решение неравенств , на понятных примерах!
Перед тем, как рассмотреть решение неравенств на примерах, разберемся с базовыми понятиями.
Общи сведения о неравенствах
Неравенством
называется выражение, в котором функции соединяются знаками отношения >, . Неравенства бывают как числовые, так и буквенные.
Неравенства с двумя знаками отношения, называются двойными, с тремя - тройными и т.д. Например:
a(x) > b(x),
a(x)
a(x) b(x),
a(x) b(x).
a(x)
Неравенства, содержащие знак > или
или - нестрогими.
Решением неравенства
является любое значение переменой, при котором это неравенство будет верно.
"Решить неравенство
" означает, что надо найти множество всех его решений. Существуют различные методы решения неравенств
. Для решения неравенства
пользуются числовой прямой, которая бесконечна. Например, решением неравенства
x > 3 есть промежуток от 3 до +, причем число 3 не входит в этот промежуток, поэтому точка на прямой обозначается пустым кружком, т.к. неравенство строгое. +
Ответ будет следующим: x (3; +).
Значение х=3 не входит в множество решений, поэтому скобка круглая. Знак бесконечности всегда выделяется круглой скобкой. Знак означает «принадлежание».
Рассмотрим как решать неравенства на другом примере со знаком :
x 2
-+
Значение х=2 входит в множество решений, поэтому скобка квадратная и точка на прямой обозначается закрашенным кружком.
Ответ будет следующим: x .

4. Решить систему ![]()
Откуда может взяться второе неравенство системы? Например, из неравенства
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.

Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.

Ответ: система противоречива.

Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7. ![]()
![]()

Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8. ![]()
![]()
![]()
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. - М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. - М., 2011. - 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Портал Естественных Наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Центр образования «Технология обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.
Неравенство - это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость, на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту полуплоскость, а в случае системы линейных неравенств - часть плоскости, ограниченную несколькими прямыми, требуется найти на чертеже.
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования , в которых требуется найти максимум или минимум функции.
Решение систем линейных неравенств с любым числом неизвестных
Сначала разберём линейные неравенства на плоскости. Рассмотрим одно неравенство с двумя переменными и :
![]() ,
,
где - коэффициенты при переменных (некоторые числа), - свободный член (также некоторое число).
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
![]() ,
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1). Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу после этого теретического экскурса.

Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :

Подставляя значение в первое уравнение, получаем
Откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .
Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:

![]() ,
,
следовательно, координаты точки B : .
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две части, лежащие справа и слева (выше и ниже) от этой прямой.
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств , то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение. Начертим прямую
Подставив в уравнение прямой , получим , а подставив , получим . Следовательно, координаты точек пересечения с осями будут A (3; 0) , B (0; 2) . Через эти точки проведём прямую (опять рисунок 1).

Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0) :
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
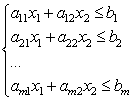
Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Решением системы линейных неравенств называется любая пара чисел (), удовлетворяющая всем неравенствам данной системы.
Геометрически решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде некоторого многоугольника, в частном случае - может быть линия, отрезок и даже точка. Если система линейных неравенств несовместна, то на плоскости не существует ни одной точки, удовлетворяющей всем неравенствам системы.
Пример 2.
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую , и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.

Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC . Это означает, что множество точек плоскости, составляющих открытый угол ABC , является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы. Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь определим полуплоскости решений для каждого неравенства (рисунок 3).

Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE . Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE .
Всё описанное выше о системах линейных неравенств с двумя неизвестными относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением неравенства с n неизвестными будет совокупность n чисел (), удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость n -мерного пространства. Решением будет многогранник решений (симплекс), ограниченный гиперплоскостями.
Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.
Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств :
Решить систему неравенств - означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.
Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x , при которых первое неравенств о (x > 1) становиться верным, а на нижней—величину х , которые являются решением второго неравенства (х > 4).
Сопоставив данные на числовых прямых , отметим, что решением для обоих неравенств будет х > 4. Ответ, х > 4.
Пример 2.
Вычисляя первое неравенство получаем -3х < -6, или x > 2, второе -х > -8, или х < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения х , при которых реализуется первое неравенство системы , а на нижнюю числовую прямую, все те значения х , при которых реализуется второе неравенство системы.
Сопоставив данные, получаем, что оба неравенства будут реализовываться при всех значениях х , размещенных от 2 до 8. Множеств значений х обозначаем двойным неравенством 2 < х < 8.
Пример 3. Найдем